题目内容
2.已知函数y=f(x)是定义在R上的增函数,且满足f(x-2)+f(-x+2)=0,若任意的x,y∈R,不等式f(x2-4x+4)+f(y2-6y)≤0恒成立,则当x≥2时,x2+y2的取值范围( )| A. | (13,49) | B. | [2,2+$\sqrt{13}$] | C. | [2,13] | D. | [4,22+6$\sqrt{13}$] |
分析 由题意可得f(-x)=-f(x),即f(x)为奇函数,则原不等式即为f(x2-4x+4)≤-f(y2-6y)=f(6y-y2),
由函数y=f(x)是定义在R上的增函数,可得x2-4x+4≤6y-y2,即有(x-2)2+(y-3)2≤9,即为圆及圆内的点,运用数形结合的思想方法,即可得到所求最值.
解答 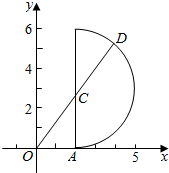 解:由f(x)满足f(x-2)+f(-x+2)=0,
解:由f(x)满足f(x-2)+f(-x+2)=0,
将x-2换为x,可得f(x)+f(-x)=0,即f(-x)=-f(x),
由不等式f(x2-4x+4)+f(y2-6y)≤0恒成立,
可得f(x2-4x+4)≤-f(y2-6y)=f(6y-y2),
由函数y=f(x)是定义在R上的增函数,可得
x2-4x+4≤6y-y2,即有(x-2)2+(y-3)2≤9,
表示圆心(2,3),半径为3的圆及圆内的点,
当x≥2时,x2+y2的几何意义为(x,y)与(0,0)的距离的平方.
如图,可得当x=2,y=0时,取得最小值,且为4;
连接OC,延长交圆于D,可得|OD|2=(3+$\sqrt{13}$)2=22+6$\sqrt{13}$.
则x2+y2的取值范围是[4,22+6$\sqrt{13}$].
故选:D.
点评 本题考查函数的奇偶性和单调性的运用,考查圆的方程及运用,以及数形结合的思想方法,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
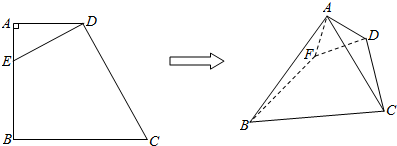
 空间四边形ABCD中,E、F分别是AB、CD的中点,AD⊥BC,且AD=4,BC=6,求异面直线EF与BC所成角的大小.
空间四边形ABCD中,E、F分别是AB、CD的中点,AD⊥BC,且AD=4,BC=6,求异面直线EF与BC所成角的大小.