题目内容
12．已知|1-4ki|=5，求实数k的值．分析 由|1-4ki|=5，可得$\sqrt{1+16{k}^{2}}$=5，解出即可得出．
解答 解：∵|1-4ki|=5，
∴$\sqrt{1+16{k}^{2}}$=5，
化为：k2=$\frac{3}{2}$，
解得k=$±\frac{\sqrt{6}}{2}$．
点评 本题考查了复数模的计算公式、方程的解法，考查了计算能力，属于基础题．
练习册系列答案
相关题目
2．已知函数y=f（x）是定义在R上的增函数，且满足f（x-2）+f（-x+2）=0，若任意的x，y∈R，不等式f（x2-4x+4）+f（y2-6y）≤0恒成立，则当x≥2时，x2+y2的取值范围（ ）
| A． | （13，49） | B． | [2，2+$\sqrt{13}$] | C． | [2，13] | D． | [4，22+6$\sqrt{13}$] |
20．用二分法求方程x2=（$\frac{1}{2}$）x-2的近似解时，所取的初始区间可以是（ ）
| A． | （0，1） | B． | （1，2） | C． | （2，3） | D． | （3，4） |
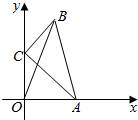在平面直角坐标系中，△ABC满足：∠C=90°，AC=2，BC=1，点A、C分别在x轴、y轴上，当点A从原点开始在x轴的正半轴上运动时，点C随着在y轴上运动．