题目内容
14.如图在直角梯形ABCD中,∠BAD=∠ABC=90°,AD=$\sqrt{3}$,BC=CD=2$\sqrt{3}$,点E是AB边上一点,现将△ADE沿边DE折起,使平面ADE⊥平面BCDE,且CD⊥AD.(1)求证:AE⊥CD;
(2)求直线AB与平面ADE所成角的大小.
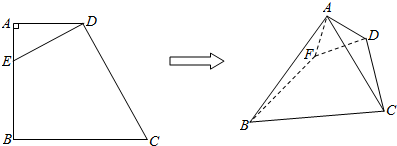
分析 (1)过A作AO⊥DE于点O,推导出AO⊥CD,CD⊥AD,由此能证明CD⊥AE.
(2)过B作BH⊥DE,交DE延长线于点H,连结AH,则∠BAH即为直线AB与平面ADE所成的角,由此能求出直线AB与平面ADE所成角.
解答 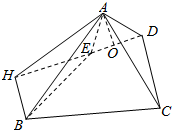 证明:(1)过A作AO⊥DE于点O,
证明:(1)过A作AO⊥DE于点O,
∵平面ADE⊥平面BCDE,平面ADE∩平面BCDE=DE,
∴AO⊥平面BCDE,∴AO⊥CD,
∵CD⊥AD,AD∩AO=A,∴CD⊥平面ADE,
∴CD⊥AE.
解:(2)过B作BH⊥DE,交DE延长线于点H,连结AH,
∵平面ADE⊥平面BCDE,平面ADE∩平面BCDE=DE,
∴BH⊥平面ADE,
∴∠BAH即为直线AB与平面ADE所成的角,
由(1)知CD⊥DE,
设AE=a,则BE=3-a,DE=$\sqrt{3+{a}^{2}}$,CE=$\sqrt{(3-{a}^{2})+12}$,
∵DE2+CD2=CE2,∴a=1,即AE=1,DE=2,BE=2,
∴△ADE≌△HBE,∴HB=$\sqrt{3}$,
∴在Rt△AHB中,∠BAH=45°,
即直线AB与平面ADE所成角为45°.
点评 本题考查异面直线垂直的证明,考查直线与平面所成角的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
4.某一考点有64个考场,考场编号为001~064,现根据考场号,采用系统抽样的方法,抽取8个考场进行监控抽查,已抽看了005号考场,则下列被抽到的考场号是( )
| A. | 050 | B. | 051 | C. | 052 | D. | 053 |
5.下列命题正确的个数是( )
①a•c=b2是a,b,c成等比数列的必要条件.
②公比q>1的等比数列的各项均大于1.
③常数列是公比为1的等比数列.
④{lg2n}}是等差数列而不是等比数列.
①a•c=b2是a,b,c成等比数列的必要条件.
②公比q>1的等比数列的各项均大于1.
③常数列是公比为1的等比数列.
④{lg2n}}是等差数列而不是等比数列.
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
2.已知函数y=f(x)是定义在R上的增函数,且满足f(x-2)+f(-x+2)=0,若任意的x,y∈R,不等式f(x2-4x+4)+f(y2-6y)≤0恒成立,则当x≥2时,x2+y2的取值范围( )
| A. | (13,49) | B. | [2,2+$\sqrt{13}$] | C. | [2,13] | D. | [4,22+6$\sqrt{13}$] |
6.已知平面α的一个法向量$\overrightarrow{n}$=(3,4,-5),点A(2,-1,3),B(1,0,4),若A∈α,B∉α,则点B到平面α的距离为( )
| A. | $\frac{\sqrt{2}}{5}$ | B. | $\frac{2\sqrt{2}}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{4}{5}$ |
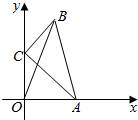 在平面直角坐标系中,△ABC满足:∠C=90°,AC=2,BC=1,点A、C分别在x轴、y轴上,当点A从原点开始在x轴的正半轴上运动时,点C随着在y轴上运动.
在平面直角坐标系中,△ABC满足:∠C=90°,AC=2,BC=1,点A、C分别在x轴、y轴上,当点A从原点开始在x轴的正半轴上运动时,点C随着在y轴上运动.