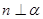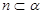题目内容
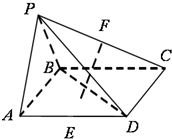
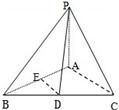
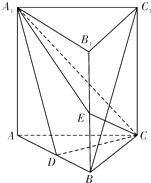
四棱锥P-ABCD底面是平行四边形,面PAB⊥面ABCD,PA=PB=AB=
AD,∠BAD=60°,E,F分别为AD,PC的中点.
(1)求证:EF∥面PAB
(2)求证:EF⊥面PBD
(3)求二面角D-PA-B的余弦值.
| 1 |
| 2 |
(1)求证:EF∥面PAB
(2)求证:EF⊥面PBD
(3)求二面角D-PA-B的余弦值.

(1)证明:取PB的中点为M连结AM,MF,因为F为PC的中点,所以FM
BC,又ABCD是平行四边形,
E为AD的中点,所以AMFE是平行四边形,
所以EF∥面PAB.
(2)因为PA=PB=AB=
AD,M是PB的中点,所以AM⊥PB,∠BAD=60°,所以AB⊥BD,
因为面PAB⊥面ABCD,所以BD⊥平面PAB,所以AM⊥BD,
又PB∩BD=B,所以AM⊥面PBD.EF∥AM,
所以EF⊥面PBD.
(3)由(2)可知BD⊥平面PAB,作BN⊥PA于N,
显然N是PA的中点,连结ND,
则∠BND就是二面角D-PA-B的平面角,
设PA=PB=AB=
AD=2,所以AN=1,AD=4,BD=
=
,
BN=
=
,所以ND=
=
,
所以二面角D-PA-B的余弦值为:
=
=
.

| ∥ |
| . |
| 1 |
| 2 |
E为AD的中点,所以AMFE是平行四边形,
所以EF∥面PAB.
(2)因为PA=PB=AB=
| 1 |
| 2 |
因为面PAB⊥面ABCD,所以BD⊥平面PAB,所以AM⊥BD,
又PB∩BD=B,所以AM⊥面PBD.EF∥AM,
所以EF⊥面PBD.
(3)由(2)可知BD⊥平面PAB,作BN⊥PA于N,
显然N是PA的中点,连结ND,
则∠BND就是二面角D-PA-B的平面角,
设PA=PB=AB=
| 1 |
| 2 |
| 42-22 |
| 12 |
BN=
| 22-12 |
| 3 |
(
|
| 15 |
所以二面角D-PA-B的余弦值为:
| BN |
| DN |
| ||
|
| ||
| 5 |


练习册系列答案
相关题目
 中,
中,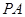 ⊥底面
⊥底面 ,四边形
,四边形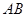 ⊥
⊥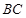 ,
,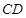 ,
,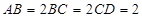 ,
,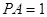 .
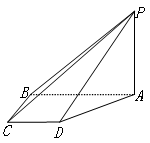
.
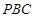 ⊥平面
⊥平面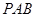 ;
;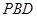 的距离;
的距离;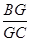 =
=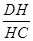 =2.求证:直线EG,FH,AC相交于一点.
=2.求证:直线EG,FH,AC相交于一点.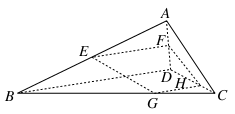

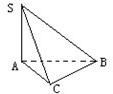
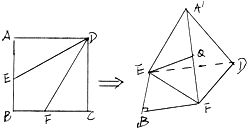
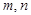 和平面
和平面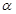 ,则
,则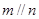 的一个必要条件是( )
的一个必要条件是( )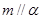 ,
,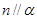
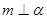 ,
,