题目内容
如图,随机地在圆内取一点,则该点落到圆内接正三角形内(阴影区域不包括边界)的概率为( )


A、
| ||||
B、
| ||||
C、
| ||||
| D、以上全错 |
考点:几何概型
专题:概率与统计
分析:先明确是几何概型中的面积类型,分别求三角形与圆的面积,然后求比值即可.
解答:
解:设落在阴影部分内接正三角形上的概率是P,圆的半径为R,
∵S圆=πR2,正三角形的面积SA=3×
×R2×sin120°=
R2
∴P=
=
.
故选B.
∵S圆=πR2,正三角形的面积SA=3×
| 1 |
| 2 |
3
| ||
| 4 |
∴P=
| SA |
| S圆 |
3
| ||
| 4 |
故选B.
点评:本题主要考查几何概型中的面积类型,基本方法是:分别求得构成事件A的区域面积和试验的全部结果所构成的区域面积,两者求比值,即为概率.

练习册系列答案
相关题目
已知f(x)=ax5-bx3+cx+2且f(5)=8,那么f(-5)等于( )
| A、-4 | B、4 | C、-8 | D、8 |
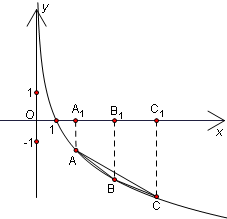 如图,A,B,C是函数
如图,A,B,C是函数