题目内容
i+i2+i3+…+i2013=( )
| A、1 | B、i | C、-i | D、-1 |
考点:复数代数形式的混合运算
专题:数系的扩充和复数
分析:利用i4n+1+i4n+2+i4n+3+i4n+4=0,即可求得答案.
解答:
解:∵i4n+1+i4n+2+i4n+3+i4n+4=i+(-1)-i+1=0,
2013=4×504+1,
∴i+i2+i3+…+i2013=504×0+i=i,
故选:B.
2013=4×504+1,
∴i+i2+i3+…+i2013=504×0+i=i,
故选:B.
点评:本题考查复数代数形式的混合运算,熟练应用i的幂的运算性质i4n+1+i4n+2+i4n+3+i4n+4=0是关键,属于基础题.

练习册系列答案
相关题目
高三年级的三个班去甲、乙、丙、丁四个工厂参加社会实践,但去何工厂可自由选择,甲工厂必须有班级要去,则不同的分配方案有( )
| A、16种 | B、18种 |
| C、37种 | D、48种 |
函数f(x)的定义域为R,其导函数f′(x)的图象如图所示,则函数f(x)( )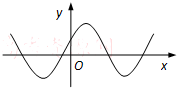

| A、有三个极值点,但无法判断有几个极大值,几个极小值 |
| B、有一个极大值点,两个极小值点 |
| C、有两个极大值点,两个极小值点 |
| D、有四个极值点,但无法判断有几个极大值,几个极小值 |
若函数f(x)=lnx-1,则f′(1)=( )
| A、0 | B、1 | C、-1 | D、e |
共轭的两个复数之和大于2的一个充要条件为( )
| A、两复数的实部都大于1 |
| B、两复数的实部都大于2 |
| C、两复数的虚部都大于1 |
| D、两复数的虚部都大于2 |
在相距4千米的A、B两点处测量目标C,若∠CAB=75°,∠CBA=60°,则A、C两点之间的距离是( )
| A、4千米 | ||
B、2
| ||
C、2
| ||
| D、2千米 |
函数f(x)=cos(x2+x)导数是( )
| A、-sin(x2+x) |
| B、-(2x+1)sin(x2+x) |
| C、-2xsin(x2+x) |
| D、(2x+1)sin(x2+x) |
某射击运动员射击所得环数ξ的分布列如下所示,则P(ξ=8)=( )
| ξ | 7 | 8 | 9 | 10 |
| P | 0.21 | m | 0.29 | 0.22 |
| A、0.31 | B、0.38 |
| C、0.41 | D、0.28 |