题目内容
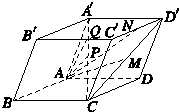 如图所示,在平行六面体ABCD-A′B′C′D′中,
如图所示,在平行六面体ABCD-A′B′C′D′中,| AB |
| a |
| AD |
| b |
| AA′ |
| c |
| a |
| b |
| c |
| AP |
| AM |
| AN |
| AQ |
分析:利用向量的中点公式和运算法则即可得出.
解答:解:连接AC,AD′.
(1)
=
(
+
)=
(
+
+
)=
(
+
+
).
(2)
=
(
+
)=
(
+2
+
)=
(
+2
+
);
(3)
=
(
+
)=
[(
+
+
)+(
+
)]=
(
+2
+2
)=
+
+
;
(4)
=
+
=
+
(
-
)═
+
=
+
+
=
+
+
.
(1)
| AP |
| 1 |
| 2 |
| AC |
| AA′ |
| 1 |
| 2 |
| AB |
| AD |
| AA′ |
| 1 |
| 2 |
| a |
| b |
| c |
(2)
| AM |
| 1 |
| 2 |
| AC |
| AD′ |
| 1 |
| 2 |
| AB |
| AD |
| AA′ |
| 1 |
| 2 |
| a |
| b |
| c |
(3)
| AN |
| 1 |
| 2 |
| AC′ |
| AD′ |
| 1 |
| 2 |
| AB |
| AD |
| AA′ |
| AD |
| AA′ |
| 1 |
| 2 |
| AB |
| AD |
| AA′ |
| 1 |
| 2 |
| a |
| b |
| c |
(4)
| AQ |
| AC |
| CQ |
| AC |
| 4 |
| 5 |
| AA′ |
| AC |
| 1 |
| 5 |
| AC |
| 4 |
| 5 |
| AA′ |
| 1 |
| 5 |
| AB |
| 1 |
| 5 |
| AD |
| 4 |
| 5 |
| AA′ |
| 1 |
| 5 |
| a |
| 1 |
| 5 |
| b |
| 4 |
| 5 |
| c |
点评:熟练掌握向量的中点公式和运算法则是解题的关键.

练习册系列答案
相关题目
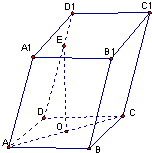 如图所示,在平行六面体ABCD-A1B1C1D1中,O为AC的中点.
如图所示,在平行六面体ABCD-A1B1C1D1中,O为AC的中点.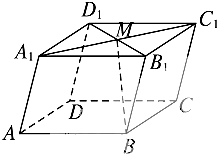 如图所示,在平行六面体ABCD-A1B1C1D1中,M为A1C1与B1D1的交点.若
如图所示,在平行六面体ABCD-A1B1C1D1中,M为A1C1与B1D1的交点.若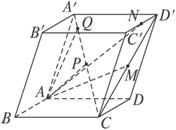
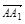 =a,
=a,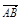 =b,
=b,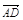 =c,M,N,P分别是AA1,BC,C1D1的中点,试用a,b,c表示以下各向量:
=c,M,N,P分别是AA1,BC,C1D1的中点,试用a,b,c表示以下各向量:
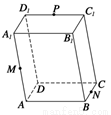
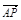 ;(2)
;(2)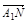 ;(3)
;(3)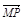 +
+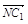 .
.