题目内容
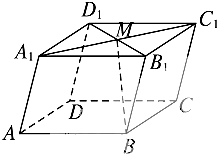如图所示，在平行六面体ABCD-A1B1C1D1中，M为A1C1与B1D1的交点．若| AB |
| a |
| AD |
| b |
| AA1 |
| c |
| BM |
| a |
| b |
| c |
分析：根据平行四边形的性质与向量的减法法则，得到
=
=
（
-
）=
（
-
）．再由向量加法的三角形法则，得到
=
+
=
+
，从而可得
=
+
（
-
），进而得到本题答案．
| B1M |
| 1 |
| 2 |
| B 1D1 |
| 1 |
| 2 |
| A1D1 |
| A1B1 |
| 1 |
| 2 |
| b |
| a |
| BM |
| BB1 |
| B1M |
| AA1 |
| B1M |
| BM |
| c |
| 1 |
| 2 |
| b |
| a |
解答：解：∵平行四边形A1B1C1D1中，对角线A1C1、B1D1相交于点M，
∴向量
=
=
（
-
），
∵平行四边形AA1B1B中，
=
=
；平行四边形AA1D1D中，
=
=
，
∴
=
（
-
），
又∵
=
=
，
∴
=
+
=
+
（
-
）=-
+
+
．
故答案为：-
+
+
∴向量
| B1M |
| 1 |
| 2 |
| B 1D1 |
| 1 |
| 2 |
| A1D1 |
| A1B1 |
∵平行四边形AA1B1B中，
| A1B1 |
| A B |
| a |
| A1D1 |
| A D |
| b |
∴
| B1M |
| 1 |
| 2 |
| b |
| a |
又∵
| BB1 |
| AA1 |
| c |
∴
| BM |
| BB1 |
| B1M |
| c |
| 1 |
| 2 |
| b |
| a |
| 1 |
| 2 |
| a |
| 1 |
| 2 |
| b |
| c |
故答案为：-
| 1 |
| 2 |
| a |
| 1 |
| 2 |
| b |
| c |
点评：本题在平行六面体中，求向量
用
、
、
表示的式子，着重考查了平行四边形与平行六面体的性质、向量的定义与加减法则等知识，属于中档题．
| BM |
| AB |
| AD |
| AA1 |
练习册系列答案
相关题目
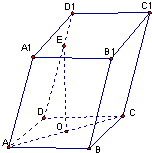如图所示，在平行六面体ABCD-A1B1C1D1中，O为AC的中点．
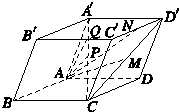如图所示，在平行六面体ABCD-A′B′C′D′中，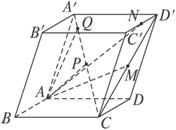
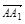=a, 
=b, 
=c,P是CA′的中点，M是CD′的中点，N是C′D′的中点，点Q在CA′上，且CQ∶QA′=4∶1,用基底a、b、c表示以下向量： 
；(2)
;(3)
;(4)
.
=a，
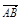=b，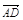
=c，M，N，P分别是AA1，BC，C1D1的中点，试用a，b，c表示以下各向量：
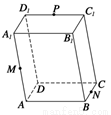
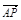；（2）
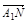；（3）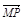
+
.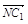