题目内容
18．若变量x，y满足约束条件$\left\{\begin{array}{l}{y≤4}\\{x+y-4≥0}\\{x-y≥0}\end{array}\right.$，则z=2x+y的最小值是（ ）| A． | 4 | B． | 6 | C． | 8 | D． | 12 |
分析 画出满足约束条件的可行域，利用目标函数的几何意义，判断目标函数经过的点，可得最优解．
解答 
解：满足约束条件$\left\{\begin{array}{l}{y≤4}\\{x+y-4≥0}\\{x-y≥0}\end{array}\right.$的可行域如下图所示：
∵目标函数z=2x+y，平移目标函数，的目标函数经过可行域的A时，取得最小值．$\left\{\begin{array}{l}{x+y=4}\\{x-y=0}\end{array}\right.$，可得A（2，2）
故在A（2，2）处目标函数达到最小值：6．
故选：B．
点评 本题考查的知识点是简单线性规划，掌握目标函数的几何意义，熟练掌握其解答过程和步骤是解答的关键．
练习册系列答案
相关题目
8．执行如图的程序框图，输出的S的值为（ ）
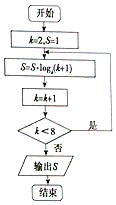
| A． | 6 | B． | 5 | C． | 4 | D． | 3 |
10．已知圆M：（x-3）2+（y-3）2=4，E，F分别为圆内接正△ABC的边AB，BC的中点，当△ABC绕圆心M转动时，则$\overrightarrow{ME}•\overrightarrow{OF}$（O为坐标原点）的取值范围是（ ）
| A． | $[{-\frac{1}{2}-6\sqrt{2}，-\frac{1}{2}+6\sqrt{2}}]$ | B． | [-6，6] | C． | $[{-\frac{1}{2}-3\sqrt{2}，-\frac{1}{2}+3\sqrt{2}}]$ | D． | [-4，4] |
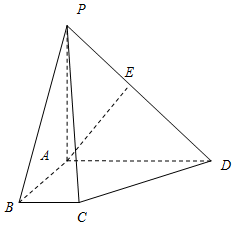在四棱锥P-ABCD中，底面ABCD是一直角梯形，PA⊥底面ABCD，∠BAD=90°，AP⊥BC，AB=BC=1，AD=AP=2，E是PD的中点．