题目内容
16．已知x＞5，则f（x）=x+$\frac{1}{x-5}$取最值时x=6．分析 由题意可得x-5＞0，可得f（x）=x+$\frac{1}{x-5}$=x-5+$\frac{1}{x-5}$+5，由基本不等式可得．
解答 解：∵x＞5，∴x-5＞0，
∴f（x）=x+$\frac{1}{x-5}$=x-5+$\frac{1}{x-5}$+5
≥2$\sqrt{（x-5）•\frac{1}{x-5}}$+5=7，
当且仅当x-5=$\frac{1}{x-5}$即x=6时取等号．
故答案为：6．
点评 本题考查基本不等式求最值，凑出可用基本不等式的形式是解决问题的关键，属基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知圆锥的底面半径为3，母线长为5，在圆锥内部放置一个内接圆柱（圆柱的一底面与圆锥的底面重合），
11．
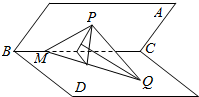如图所示，二面角A-BC-D的大小为45°，P为平面ABC内一点，Q为平面BCD内一点，M为BC上一点，已知P在平面BCD内的射影恰好在线段MQ上，设PM=$\sqrt{2}$，∠CMQ=45°，直线PQ与平面BCD所成的角为30°，则PQ的长为（ ）
如图所示，二面角A-BC-D的大小为45°，P为平面ABC内一点，Q为平面BCD内一点，M为BC上一点，已知P在平面BCD内的射影恰好在线段MQ上，设PM=$\sqrt{2}$，∠CMQ=45°，直线PQ与平面BCD所成的角为30°，则PQ的长为（ ）| A． | $\frac{2}{3}\sqrt{6}$ | B． | $\frac{3}{4}\sqrt{6}$ | C． | $\frac{4}{3}\sqrt{2}$ | D． | $\frac{3}{2}\sqrt{2}$ |