题目内容

函数y=x2的值域为
 
（用区间表示）．
考点：函数的值域
专题：函数的性质及应用
分析：根据x2的范围求得y的范围，确定函数的值域．
解答： 解：∵x2≥0，
∴函数的值域为[0，+∞），
故答案为：[0，+∞）．
点评：本题主要考查了函数的值域问题．属基础题．
练习册系列答案
相关题目
已知无穷等比数列{an}，a1=1，an=k（an+1+an+2+…），n∈N，则实数k的取值范围
 
．
若函数f（x）=ax3-4x在[-4，-1]上单调递增，则实数a的取值范围是
 
．
{an}通项为an=n2+kn+2（n∈N*），又{an}递增，则实数k的取值范围是
 
．
直线l1：y=x+a和l2：y=x+b将以原点圆心，1为半径的圆分成长度相等的四段弧，则a2+b2=
 
．
命题“若a＞b，则a-8＞b-8”的逆否命题是
 
．
已知i是虚数单位，z=1+i，
.
z
为z的共轭复数，则复数
z2
.
z
在复平面上对应的点的坐标为（　　）
A、（1，1）
B、（-1，-1）
C、（-1，1）
D、（1，-1）
下列几个选项，哪个函数是幂函数（　　）
A、y=x2
B、y=2x2
C、y=x2+x
D、y=
3
x
如图，不等式x2-y2-4x-2y+3≥0表示的平面区域是（　　）
A、
B、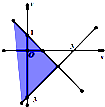
C、
D、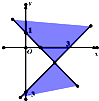

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网