题目内容
1. 已知函数f(x)=|x2-2x|.
已知函数f(x)=|x2-2x|.(1)在给出的坐标系中作出y=f(x)的图象;
(2)根据图象写出函数f(x)的单调区间和值域;
(3)若集合{x|f(x)=a}恰有三个元素,求实数a的值.
分析 (1)由f(x)=|x2-2x|=$\left\{\begin{array}{l}{{x}^{2}-2x,x≥2或x≤0}\\{2x-{x}^{2},0<x<2}\end{array}\right.$,能作出函数y=f(x)的图象.
(2)结合f(x)的图象,能求出函数f(x)的单调区间和值域.
(3)由题意得,方程f(x)=a恰有三个不等实根,由此结合直线y=a的图象能求出实数a的值.
解答 解:(1)∵f(x)=|x2-2x|=$\left\{\begin{array}{l}{{x}^{2}-2x,x≥2或x≤0}\\{2x-{x}^{2},0<x<2}\end{array}\right.$.
∴函数y=f(x)的图象如下图:
(2)结合图象得:
函数的单调增区间为[0,1],[2,+∞),单减区间为(-∞,0],[1,2].
函数的值域为[0,+∞).
(3)∵集合{x|f(x)=a}恰有三个元素,
∴由题意得,方程f(x)=a恰有三个不等实根,
结合直线y=a的图象可知,实数a的值为1.
点评 本题考查函数图象的作法、函数的单调区间及值域的求法、实数值的求法,是中档题,解题时要认真审题,注意函数性质的合理运用.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案
相关题目
12.某校学习小组开展“学生数学成绩与化学成绩的关系”的课题研究,对该校高二年级800名学生上学期期 数学和化学成绩,按优秀和不优秀分类得结果:数学和化学都优秀的有60人,数学成绩优秀但化学不优秀的有140人,化学成绩优秀但数学不优秀的有100人.
(Ⅰ)补充完整表格并判断能否在犯错概率不超过0.001前提下认为该校学生的数学成绩与化学成绩有关系?
(Ⅱ)现有4名成员甲、乙、丙、丁随机分成两组,每组2人,一组负责收集成绩,另一组负责数据处理.求学生甲分到负责收集成绩组,学生乙分到负责数据处理组的概率.
附:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$.
(Ⅰ)补充完整表格并判断能否在犯错概率不超过0.001前提下认为该校学生的数学成绩与化学成绩有关系?
| 数学优秀 | 数学不优秀 | 总计 | |
| 化学优秀 | 60 | 100 | 160 |
| 化学不优秀 | 140 | 500 | 640 |
| 总计 | 200 | 600 | 800 |
| p(K2>k0) | 0.010 | 0.005 | 0.001 |
| k0 | 6.635 | 7.879 | 10.828 |
9. 已知在四面体ABCD中,E、F分别是AC、BD的中点,若CD=2,AB=4,EF⊥CD,则EF与AB所成的角为( )
已知在四面体ABCD中,E、F分别是AC、BD的中点,若CD=2,AB=4,EF⊥CD,则EF与AB所成的角为( )
 已知在四面体ABCD中,E、F分别是AC、BD的中点,若CD=2,AB=4,EF⊥CD,则EF与AB所成的角为( )
已知在四面体ABCD中,E、F分别是AC、BD的中点,若CD=2,AB=4,EF⊥CD,则EF与AB所成的角为( )| A. | 90° | B. | 45° | C. | 60° | D. | 30° |
10.设数列{an}的前n项和为Sn,a4=7且4Sn=n(an+an+1),则Sn-6an的最小值为( )
| A. | -36 | B. | -30 | C. | -27 | D. | -20 |
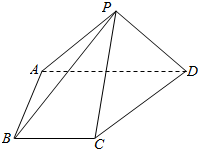 如图,四棱锥P-ABCD中,平面PAD⊥底面ABCD,PA⊥PD,PA=PD,BC∥AD,AB⊥AD,AD=2AB=2BC=2.
如图,四棱锥P-ABCD中,平面PAD⊥底面ABCD,PA⊥PD,PA=PD,BC∥AD,AB⊥AD,AD=2AB=2BC=2.