题目内容
各棱长均为a的三棱锥中，任意一个顶点到其对应面的距离为 ．
考点：棱锥的结构特征
专题：空间位置关系与距离
分析：在三棱锥S-ABC中，各棱长均为a，取BC中点D，连结AD，AD=
=
a，过S作SO⊥底面ABC，交AD于O，AO=
AD=
a，由此利用勾股定理能求出任意一个顶点到其对应面的距离．
a2-
|
| ||
| 2 |
| 2 |
| 3 |
| ||
| 3 |
解答：
解：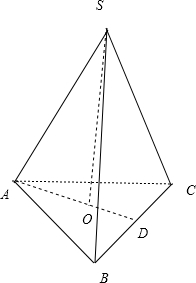
如图，在三棱锥S-ABC中，各棱长均为a，
取BC中点D，连结AD，
则AD=
=
a，
过S作SO⊥底面ABC，交AD于O，
则AO=
AD=
a，
∴SO=
=
=
a．
∴任意一个顶点到其对应面的距离为：
d=SO=
a．
故答案为：
a．
如图，在三棱锥S-ABC中，各棱长均为a，取BC中点D，连结AD，
则AD=
a2-
|
| ||
| 2 |
过S作SO⊥底面ABC，交AD于O，
则AO=
| 2 |
| 3 |
| ||
| 3 |
∴SO=
| SA2-AO2 |
a2-
|
| ||
| 3 |
∴任意一个顶点到其对应面的距离为：
d=SO=
| ||
| 3 |
故答案为：
| ||
| 3 |
点评：本题考查三棱锥中顶点到对面距离的求法，是中档题，解题时要认真审题，注意空间思维能力的培养．
练习册系列答案
相关题目
如图所示，四边形ABCD是边长为1的正方形，M、N分别是DA、BC上的点，且MN∥AB，现沿MN折起，使平面DCNM⊥平面ABNM．