题目内容
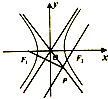 设双曲线
设双曲线| x2 |
| a2 |
| y2 |
| b2 |
| A、(2,+∞) | ||
| B、(3,+∞) | ||
C、(1,
| ||
| D、(1,2) |
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:确定M,F1,F2的坐标,进而由
•
<0,结合abc的关系可得关于ac的不等式,利用离心率的定义可得范围.
| PF1 |
| PF2 |
解答:
解:设直线方程为y=
(x-c),与双曲线
-
=1(a>0,b>0)联立,可得交点坐标为P(
,-
)
∵F1(-c,0),F2(c,0),
∴
=(-
,
),
=(
,
),
由题意可得
•
<0,即
-
<0,
化简可得b2<3a2,即c2-a2<3a2,
故可得c2<4a2,c<2a,可得e=
<2,
∵e>1,∴1<e<2
故选:D.
| b |
| a |
| x2 |
| a2 |
| y2 |
| b2 |
| c |
| 2 |
| bc |
| 2a |
∵F1(-c,0),F2(c,0),
∴
| PF1 |
| 3c |
| 2 |
| bc |
| 2a |
| PF2 |
| c |
| 2 |
| bc |
| 2a |
由题意可得
| PF1 |
| PF2 |
| b2c2 |
| 4a2 |
| 3c2 |
| 4 |
化简可得b2<3a2,即c2-a2<3a2,
故可得c2<4a2,c<2a,可得e=
| c |
| a |
∵e>1,∴1<e<2
故选:D.
点评:本题考查双曲线的离心率,考查学生解方程组的能力,属中档题.

练习册系列答案
相关题目
如图,该程序框图所输出的结果是( )


| A、16 | B、30 | C、31 | D、32 |
不等式组
所表示的平面区域的面积等于( )
|
A、
| ||
B、
| ||
C、
| ||
D、
|
方程4x2-y2+4x+2y=0表示的曲线是( )
| A、一个点 |
| B、两条互相平行的直线 |
| C、两条互相垂直的直线 |
| D、两条相交但不垂直的直线 |
已知实数x,y满足约束条件
,则z=x+2y的最小值为( )
|
A、
| ||||
| B、11 | ||||
| C、1 | ||||
| D、2 |
运行如图所示程序框图,输出的n值为( )


| A、2 | B、3 | C、4 | D、5 |
在等差数列函数{an}中,a4+a5+a6=15,则a2+a8=( )
| A、5 | B、10 | C、12 | D、15 |