题目内容
方程4x2-y2+4x+2y=0表示的曲线是（ ）
| A、一个点 |
| B、两条互相平行的直线 |
| C、两条互相垂直的直线 |
| D、两条相交但不垂直的直线 |
考点：轨迹方程
专题：计算题,直线与圆
分析：方程4x2-y2+4x+2y=0可化为（2x+y）（2x-y+2）=0，即可得出结论．
解答：
解：方程4x2-y2+4x+2y=0可化为（2x+y）（2x-y+2）=0，
∴2x+y=0或2x-y+2=0，
∴方程4x2-y2+4x+2y=0表示的曲线是两条相交但不垂直的直线．
故选：D．
∴2x+y=0或2x-y+2=0，
∴方程4x2-y2+4x+2y=0表示的曲线是两条相交但不垂直的直线．
故选：D．
点评：本题考查轨迹方程，方程4x2-y2+4x+2y=0化为（2x+y）（2x-y+2）=0，是解题的关键．
练习册系列答案
七彩题卡口算应用一点通系列答案
相关题目
如果将函数y=
cos2x+sin2x（x∈R）的图象向左平移m（m＞0）个单位后，所得图象对应的函数为偶函数，那么m的最小值为（ ）
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
下列函数是幂函数的是（ ）
| A、y=2x2 | ||
| B、y=x3+x | ||
C、y=x
| ||
| D、y=3x |
数列1+
，2+
，3+
，…，n+
，…的前n项和是（ ）
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 2n |
A、sn=
| ||||
B、sn=
| ||||
C、sn=
| ||||
D、sn=
|
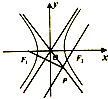设双曲线| x2 |
| a2 |
| y2 |
| b2 |
| A、（2，+∞） | ||
| B、（3，+∞） | ||
C、（1，
| ||
| D、（1，2） |
已知函数f（x）=
，若关于x的方程f（x）-kx+k=0有且只有一个实根，则实数k的取值范围是（ ）
|
| A、k≤0或k＞1 | ||||||||
| B、k＞1或k=0或k＜-1 | ||||||||
C、k＞
| ||||||||
D、k＞
|
已知函数f（x）=
若关于x 的方程f（x）=kx有两个不同的实根，则数k的取值范围是（ ）
|
| A、（0，1） |
| B、[0，2] |
| C、（0，1] |
| D、（0，2] |
函数y=sinx是（ ）
| A、最小正周期为2π的偶函数 |
| B、最小正周期为π的偶函数 |
| C、最小正周期为2π的奇函数 |
| D、最小正周期为π的奇函数 |