题目内容
动直线x=a与函数f(x)=6sinxcosx和函数g(x)=6cos2x-3的图象分别交于A,B两点,则|AB|的最大值为( )
| A、3 | ||
B、3
| ||
C、3
| ||
| D、6 |
考点:正弦函数的图象,二倍角的正弦,二倍角的余弦,余弦函数的图象
专题:函数的性质及应用
分析:首先化简f(x)、g(x),然后根据动直线x=a与函数f(x)=6sinxcosx和函数g(x)=6cos2x-3的图象分别交于A,B两点,可得|AB|=|f(x)-g(x)|,将两个函数的解析式代入化简为正弦型函数,再由正弦型函数的性质即可得到结论.
解答:
解:f(x)=6sinxcosx=3sin2x,g(x)=6cos2x-3=3cos2x,
所以|AB|=|f(x)-g(x)|
=|3sin2x-3cos2x|
=3
|sin(2x-
)|
则sin(2x-
)=±1时,
|AB|的最大值为3
.
故选:B.
所以|AB|=|f(x)-g(x)|
=|3sin2x-3cos2x|
=3
| 2 |
| π |
| 4 |
则sin(2x-
| π |
| 4 |
|AB|的最大值为3
| 2 |
故选:B.
点评:本题主要考查了三角函数的二倍角公式,正弦函数、余弦函数的图象和性质,属于基础题.

练习册系列答案
相关题目
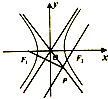 设双曲线
设双曲线| x2 |
| a2 |
| y2 |
| b2 |
| A、(2,+∞) | ||
| B、(3,+∞) | ||
C、(1,
| ||
| D、(1,2) |
若关于x的方程x2+ax+a2-1=0有一个正根和一个负根,则实数a的取值范围为( )
A、-
| ||||||||
B、-
| ||||||||
| C、-1≤a≤1 | ||||||||
| D、-1<a<1 |
三边长分别为4,5,6的三角形的形状是( )
| A、锐角三角形 |
| B、直角三角形 |
| C、钝角三角形 |
| D、以上答案均有可能 |
函数y=sinx是( )
| A、最小正周期为2π的偶函数 |
| B、最小正周期为π的偶函数 |
| C、最小正周期为2π的奇函数 |
| D、最小正周期为π的奇函数 |