题目内容
已知向量
=（4，-3），向量
=（2，1），若
-t
与
的夹角为45°，求实数t的值．
| a |
| b |
| a |
| b |
| b |
考点：平面向量数量积的坐标表示、模、夹角
专题：平面向量及应用
分析：由已知得
-t
，由
-t
与
的夹角为45°，用坐标表示（
-t
）•
，得出关于t的方程，解方程即得t的值．
| a |
| b |
| a |
| b |
| b |
| a |
| b |
| b |
解答：
解：向量
=（4，-3），向量
=（2，1），
∴
-t
=（4-2t，-3-t）；
又∵
-t
与
的夹角为45°，
∴（
-t
）•
=|
-t
|×|
|cos45°，
即2（4-2t）+1×（-3-t）=
×
×
，
化简，得1-t=
×
，
即
，
解得t=-1；
∴t的值是-1．
| a |
| b |
∴
| a |
| b |
又∵
| a |
| b |
| b |
∴（
| a |
| b |
| b |
| a |
| b |
| b |
即2（4-2t）+1×（-3-t）=
| (4-2t)2+(-3-t)2 |
| 5 |
| ||
| 2 |
化简，得1-t=
| ||
| 2 |
| t2-2t+5 |
即
|
解得t=-1；
∴t的值是-1．
点评：本题考查了平面向量的应用问题，解题时应利用坐标表示写出数量积（
-t
）•
，得到关于t的方程，解方程即可，是基础题．
| a |
| b |
| b |
练习册系列答案
科学实验活动册系列答案
相关题目
复数
•i2014（i是虚数单位）为纯虚数，则实数a的值为（ ）
| 2a+i |
| 1-2i |
A、
| ||
B、-
| ||
| C、1 | ||
| D、-1 |
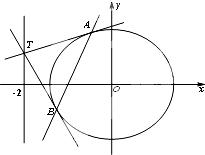设点P为圆C1：x2+y2=2上的动点，过点P作x轴的垂线，垂足为Q．动点M满足
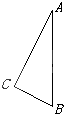已知直角三角形ABC的斜边长AB=2，现以斜边AB为轴旋转一周，得旋转体．