题目内容

设
e1
，
e2
为单位向量，其中
a
=2
e1
+
e2
，
b
=
e2
，且
a
在
b
上的投影为2，则
e1
与
e2
的夹角为（　　）
A、
π
6
B、
π
4
C、
π
3
D、
π
2
考点：平面向量数量积的运算
专题：平面向量及应用
分析：利用数量积运算、投影的意义即可得出．
解答： 解：设θ为
e1
与
e2
的夹角，则
a
•
b
|
b
|
=
(2
e1
+
e2
)•
e2
|
e2
|
=
2
e1
•
e2
+
e2
2
1
=
2×|
e1
| |
e2
|cosθ+1
1
=2cosθ+1=2，
解得：cosθ=
1
2
，
则θ=
π
3
．
故选：C．
点评：本题考查了数量积运算、投影的意义，属于基础题．
练习册系列答案
相关题目
已知f（x）是定义在R上的奇函数．当x＞0时，f（x）=2x3-9x2+12x，则不等式f（x）≥-f（-1）在R上的解集是
 
．
已知某几何的三视图如图所示，则该几何体的体积为（　　）
A、
8
3
B、8
C、
4
3
5
D、4
5
若实数x、y满足条件
x-y≤0
x+y≥0
y≤1
，则x+2y的最大值是（　　）
A、1B、2C、3D、4
有关函数单调性的叙述中，正确的是（　　）
A、y=-
2
x
 在定义域上为增函数
B、y=
1
x2+1
在[0，+∞）上为增函数
C、y=-3x2-6x的减区间为[-1，+∞）
D、y=ax+3在（-∞，+∞）上必为增函数
下列函数中，在区间（-1，1）上是减函数的是（　　）
A、y=2-3x2
B、y=lnx
C、y=
1
x-2
D、y=sinx
已知a1=1，如图给出程序框图，当k=5时，输出的S=（　　）
A、
4
9
B、
5
11
C、
10
11
D、
6
13
已知f（x）=
x+1，x∈[-1，0)
x2+1．x∈[0，1]
，则下列叙述中不正确的一项是（　　）
A、
f（x-1）的图象
B、
|f（x）|的图象
C、
f（-x）的图象
D、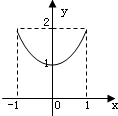
f（|x|）的图象
在等比数列{an}中，a1=27，q=-
1
3
，则S3=（　　）
A、21B、22C、12D、28

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网