题目内容
 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<| π |
| 2 |
| 3 |
| 2 |
| π |
| 2 |
(1)求函数y=f(x)的解析式;
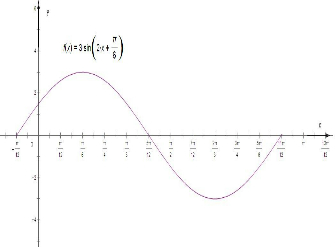
(2)用“五点法”作出此函数在[0,π]上的图象.
考点:由y=Asin(ωx+φ)的部分图象确定其解析式,五点法作函数y=Asin(ωx+φ)的图象
专题:三角函数的图像与性质
分析:(1)通过函数的最大值点求出A,最大值与最小值的横坐标求出函数的周期,然后求出ω,利用函数经过(0,
),以及φ的范围,求出φ,然后得到函数y=f(x)的解析式;
(2)分别令2x+
=0,
,π,
,2π,得到相应的x的值及y的值,再描点即可.
| 3 |
| 2 |
(2)分别令2x+
| π |
| 6 |
| π |
| 2 |
| 3π |
| 2 |
解答:
解:(1)由题意可得A=3,由在y轴右侧的第一个最大值点和最小值点分别为(x0,3),(x0+
,-3)得
T=x0+
-x0=
,
∴T=π从而ω=2,
又图象与y轴交于点(0,
),
∴
=3sinφ⇒sinφ=
,
由于|φ|<
,
∴φ=
,
函数的解析式为f(x)=3sin(2x+
).
(2)解:列表
图象如图:
| π |
| 2 |
| 1 |
| 2 |
| π |
| 2 |
| π |
| 2 |
∴T=π从而ω=2,
又图象与y轴交于点(0,
| 3 |
| 2 |
∴
| 3 |
| 2 |
| 1 |
| 2 |
由于|φ|<
| π |
| 2 |
∴φ=
| π |
| 6 |
函数的解析式为f(x)=3sin(2x+
| π |
| 6 |
(2)解:列表
2x+
| 0 |
| π |
| 2π | ||||||||||
| x | -
|
|
|
|
| ||||||||||
| y | 0 | 3 | 0 | -3 | 0 |

点评:本题考查三角函数的解析式的求法,注意A,ω,φ的求法,考查五点法作函数y=Asin(ωx+φ)的图象,属于中档题.

练习册系列答案
相关题目
已知命题p为真命题,命题q为假命题,则( )
| A、p∧(¬q)为真 |
| B、p∧q为真 |
| C、(¬p)∨q为真 |
| D、(¬p)∧q为真 |
