题目内容
16.${(\frac{1+i}{1-i})^{2006}}$=( )| A. | 1 | B. | -1 | C. | i | D. | -i |
分析 根据复数的混合运算法则计算即可
解答 解:$\frac{1+i}{1-i}$=$\frac{(1+i)^{2}}{(1-i)(1+i)}$=$\frac{2i}{2}$=i,
i2=-1,
∴${(\frac{1+i}{1-i})^{2006}}$=(i)2006=(-1)1003=-1,
故选:B
点评 本题考查了复数的混合运算,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.已知向量$\overrightarrow{a}$=(an,2),$\overrightarrow{b}$=(an+1,$\frac{2}{5}$),且a1=1,若数列{an}的前n项和为Sn,且$\overrightarrow{a}$∥$\overrightarrow{b}$,则Sn=( )
| A. | $\frac{5}{4}$[1-($\frac{1}{5}$)n] | B. | $\frac{1}{4}$[1-($\frac{1}{5}$)n] | C. | $\frac{1}{4}$[1-($\frac{1}{5}$)n-1] | D. | $\frac{5}{4}$[1-($\frac{1}{5}$)n-1] |
8.若$C_n^{10}=C_n^8$,则$C_{20}^n$=( )
| A. | 380 | B. | 190 | C. | 18 | D. | 9 |
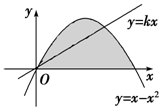 如图直线y=kx及抛物线y=x-x2
如图直线y=kx及抛物线y=x-x2