��Ŀ����
2����Ԫʱ�ڽܳ�����ѧ��������������ѧ��������Ԫ��������С������ζΡ���һ�����⡰�����������ٰ�ʮ���������һ�Ρ��ʣ�ͬ�⣩֮���ʵ��ӣ�ÿ�������α������������ȼ��ڲ��������Σ�����̽���ˡ����������е���һ�ζ⣨����һ�Ρ�����ָ����1������һ��3��������һ��6���������������ĶѶ⣬��Ҳ�����Ƕ⣬��ͼ����ʾ�ڶ��㿪ʼ��ÿ�������������������������Ƕ�ײ�����������Ϊ120��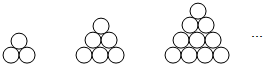
���� �����⣬��n����������Ϊ1+2+��+n=$\frac{n��n+1��}{2}$������1+3+6+��+$\frac{n��n+1��}{2}$=680�����n�����ɵó����ۣ�
��� �⣺�����⣬��n����������Ϊ1+2+��+n=$\frac{n��n+1��}{2}$��
��1+3+6+��+$\frac{n��n+1��}{2}$=680��
��Ϊ$\frac{1}{2}$[$\frac{1}{6}$n��n+1����2n+1��+$\frac{1}{2}$n��n+1��]=$\frac{1}{6}$n��n+1����n+2��=680��
����n��n+1����n+2��=15��16��17��
��n=15����$\frac{n��n+1��}{2}$=120��
�ʴ�Ϊ��120
���� ���⿼��������ѧ֪ʶ���ʵ�����⣬����ѧ������������������ѧ���ļ��������������е��⣮

��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ
10��Բx2+y2=-4y��Բ��x-1��2+y2=1��λ�ù�ϵ�ǣ�������
| A�� | �ཻ | B�� | ���� | C�� | ���� | D�� | ���� |
17����֪a��b����ʵ������ô��$\sqrt{a}$��$\sqrt{b}$���ǡ�lna��lnb���ģ�������
| A�� | ��ֲ���Ҫ���� | B�� | ��Ҫ��������� | ||
| C�� | ��Ҫ���� | D�� | �Ȳ����Ҳ����Ҫ���� |