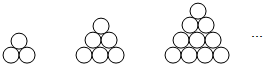
题目内容
7.已知f(n)=1+$\frac{1}{2}+\frac{1}{3}+…+\frac{1}{n}({n∈{N^*}})$ 经计算得f(2)=$\frac{3}{2},f(4)>2,f(8)>\frac{5}{2},f({16})>3,f({32})>\frac{7}{2}$,…,观察上述结果,可归纳出的一般结论为f(2n)≥$\frac{n+2}{2}$(n∈N*).
分析 由题意f(4)>2,可化为f(22)>$\frac{2+2}{2}$,f(8)>$\frac{5}{2}$,可化为f(23)>$\frac{2+3}{2}$,即可得出结论.
解答 解:观察已知中等式:
得f(22)>$\frac{2+2}{2}$,f(23)>$\frac{2+3}{2}$,
…,
则f(2n)≥$\frac{n+2}{2}$(n∈N*)
故答案为:f(2n)≥$\frac{n+2}{2}$(n∈N*)
点评 本题考查归纳推理,把已知的式子变形找规律是解决问题的关键,属基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.近年来空气污染是一个生活中重要的话题,PM2.5就是其中一个重要指标.各省、市、县均要进行实时监测,某市2015年11月的PM2.5浓度统计如图所示.
(1)请完成频率分布表;
(2)专家建议,空气质量为优、良、轻度污染时可正常进行户外活动,中度污染及以上时,取消一切户外活动,在2015年11月份,该市某学校进行了连续两天的户外拔河比赛,求拔河比赛能正常进行的概率.
| 日期 | PM2.5浓度 | 日期 | PM2.5浓度 | 日期 | PM2.5浓度 |
| 11-1 | 137 | 11-11 | 144 | 11-21 | 40 |
| 11-2 | 143 | 11-12 | 166 | 11-22 | 42 |
| 11-3 | 145 | 11-13 | 197 | 11-23 | 35 |
| 11-4 | 193 | 11-14 | 194 | 11-24 | 53 |
| 11-5 | 133 | 11-15 | 219 | 11-25 | 88 |
| 11-6 | 22 | 11-16 | 41 | 11-26 | 29 |
| 11-7 | 22 | 11-17 | 90 | 11-27 | 199 |
| 11-8 | 57 | 11-18 | 46 | 11-28 | 287 |
| 11-9 | 111 | 11-19 | 80 | 11-29 | 291 |
| 11-10 | 134 | 11-20 | 67 | 11-30 | 452 |
| 空气质量指数类别 | PM2.5 24小时浓度均值 | 频数 | 频率 |
| 优 | 0-35 | 4 | $\frac{2}{15}$ |
| 良 | 36-75 | 7 | $\frac{7}{30}$ |
| 轻度污染 | 76-115 | 4 | |
| 中度污染 | 116-150 | 6 | |
| 重度污染 | 151-250 | ||
| 严重污染 | 251-500 | ||
| 合计 | / | 30 | 1 |
15.复数z满足z(l-i)=-1-i,则|z+1|=( )
| A. | 0 | B. | 1 | C. | $\sqrt{2}$ | D. | 2 |