题目内容
已知函数f(x)=sinxcosx-m(sinx+cosx)
(1)若m=1,求函数在(0,
)上的单调区间;
(2)若函数在区间(
,π)上是单调递减函数,求m的取值范围.
(1)若m=1,求函数在(0,
| π |
| 2 |
(2)若函数在区间(
| π |
| 2 |
考点:三角函数中的恒等变换应用,正弦函数的图象
专题:函数的性质及应用,三角函数的图像与性质
分析:(1)m=1时,令sinx+cosx=t,可得f(t)=
(t-1)2-
,从而有
≤sin(x+
)≤1,可解得单调递增区间[2kπ,2kπ+
],k∈Z.
(2)令sinx+cosx=t,有f(t)=
(t-m)2-
-
,当t=m时,函数取得最小值,t∈(-∞,m)函数是减函数.由
sin(
+
)=1,
sin(π+
)=-1,可得m的取值范围.
| 1 |
| 2 |
| 3 |
| 2 |
| ||
| 2 |
| π |
| 4 |
| π |
| 2 |
(2)令sinx+cosx=t,有f(t)=
| 1 |
| 2 |
| 1 |
| 2 |
| m2 |
| 2 |
| 2 |
| π |
| 2 |
| π |
| 4 |
| 2 |
| π |
| 4 |
解答:
解:(1)∵f(x)=sinxcosx-m(sinx+cosx),
∴m=1时,f(x)=sinxcosx-(sinx+cosx),
令sinx+cosx=t,
t∈[-
,
],则sinxcosx=
,
∴f(t)=
-t=
(t2-2t)-
=
(t-1)2-1,
那么当t=1,y取得最小值=-1,
当t=-
,y取得最大值
+
,
∴t∈[1,
]上时单调递增.t∈[-
,1]上时单调递减,
∴1≤
sin(x+
)≤
,有
≤sin(x+
)≤1,
∴可解得2kπ≤x≤2kπ+
,k∈Z,
∴单调递增区间[2kπ,2kπ+
],k∈Z在[0,
]上单调递增.
(2)令sinx+cosx=t,
t∈[-
,
],则sinxcosx=
,
∴f(t)=
-mt=
(t2-2mt)-
=
(t-m)2-
-
,
当t=m,m∈[-
,
]时,函数取得最小值,t∈(-
,m)函数是减函数.
x∈(
,π)时,函数是减函数,sinπcosπ-m(sinπ+cosπ)≥-
-
,
∴m∈R.可得m∈[-
,
].
当|m|>
时,t=±
,函数取得最小值,可得:x=
,或x=
不满足题意.
综上:m∈[-
,
].
∴m=1时,f(x)=sinxcosx-(sinx+cosx),
令sinx+cosx=t,
t∈[-
| 2 |
| 2 |
| t2-1 |
| 2 |
∴f(t)=
| t2-1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
那么当t=1,y取得最小值=-1,
当t=-
| 2 |
| 1 |
| 2 |
| 2 |
∴t∈[1,
| 2 |
| 2 |
∴1≤
| 2 |
| π |
| 4 |
| 2 |
| ||
| 2 |
| π |
| 4 |
∴可解得2kπ≤x≤2kπ+
| π |
| 4 |
∴单调递增区间[2kπ,2kπ+
| π |
| 4 |
| π |
| 4 |
(2)令sinx+cosx=t,
t∈[-
| 2 |
| 2 |
| t2-1 |
| 2 |
∴f(t)=
| t2-1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| m2 |
| 2 |
当t=m,m∈[-
| 2 |
| 2 |
| 2 |
|
x∈(
| π |
| 2 |
| 1 |
| 2 |
| m2 |
| 2 |
∴m∈R.可得m∈[-
| 2 |
| 2 |
当|m|>
| 2 |
| 2 |
| π |
| 4 |
| 5π |
| 4 |
综上:m∈[-
| 2 |
| 2 |
点评:本题主要考察了三角函数中的恒等变换应用,三角函数的图象与性质,函数值域的求法,考察了转化思想,属于中档题.

练习册系列答案
相关题目
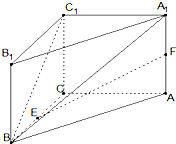 在直三棱柱ABC-A1B1C1中,CA=CB=CC1=2,∠ACB=90°,E、F分别是BC A1A的中点.
在直三棱柱ABC-A1B1C1中,CA=CB=CC1=2,∠ACB=90°,E、F分别是BC A1A的中点.