题目内容
记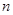 项正项数列为
项正项数列为 ,其前
,其前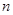 项积为
项积为 ,定义
,定义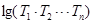 为“相对叠乘积”,如果有2013项的正项数列
为“相对叠乘积”,如果有2013项的正项数列 的“相对叠乘积”为
的“相对叠乘积”为 ,则有2014项的数列
,则有2014项的数列 的“相对叠乘积”为_______。
的“相对叠乘积”为_______。
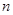 项正项数列为
项正项数列为 ,其前
,其前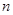 项积为
项积为 ,定义
,定义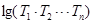 为“相对叠乘积”,如果有2013项的正项数列
为“相对叠乘积”,如果有2013项的正项数列 的“相对叠乘积”为
的“相对叠乘积”为 ,则有2014项的数列
,则有2014项的数列 的“相对叠乘积”为_______。
的“相对叠乘积”为_______。
试题分析:根据题意,由于
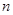 项正项数列为
项正项数列为 ,其前
,其前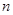 项积为
项积为 ,定义
,定义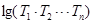 为“相对叠乘积”那么可知有2013项的正项数列
为“相对叠乘积”那么可知有2013项的正项数列 的“相对叠乘积”为
的“相对叠乘积”为 ,即为
,即为
,故答案为4027.
点评:
本题考查数列的前n项和的求法,解题时要认真审题,注意准确理解“叠乘积”的概念

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案
相关题目
 的前
的前 项和
项和 ,满足:
,满足: .
. ;
; 的满足
的满足 ,
, 为数列
为数列 的前
的前 .
. 是函数
是函数 且
且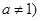 的图像上一点,等比数列
的图像上一点,等比数列 的前
的前 项的和为
项的和为 ;数列
;数列
 的首项为
的首项为 ,且前
,且前 满足
满足
 .
. 的前
的前 ,问
,问 的最小正整数
的最小正整数 的前
的前 项和
项和 满足
满足 ,等差数列
,等差数列 满足
满足 ,
, .
. ,数列
,数列 的前
的前 ,求证
,求证 .
. 满足:
满足: ,数列
,数列 满足
满足 .
. 求
求 的值及
的值及 的等比数列,问是否存在正实数
的等比数列,问是否存在正实数 ,使得数列
,使得数列 的前
的前 项和
项和 (用n,
(用n, 表示).
表示).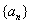 中,
中,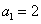 ,
,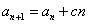 (
(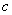 是常数,
是常数,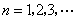 ),且
),且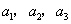 成公比不为
成公比不为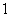 的等比数列,则
的等比数列,则 中,
中, ,则
,则 的三边长
的三边长 ,满足
,满足
 之间插入2011个数,使这2013个数构成以
之间插入2011个数,使这2013个数构成以 为首项的等差数列
为首项的等差数列 ,且它们的和为
,且它们的和为 ,求的最小值;
,求的最小值; ,且
,且 ,求满足不等式
,求满足不等式 的所有
的所有 的值;
的值; 满足
满足 ,证明:数列
,证明:数列 中的任意连续三项为边长均可以构成直角三角形,且
中的任意连续三项为边长均可以构成直角三角形,且 是正整数.
是正整数. 的前n项和
的前n项和
 ,则
,则 ( )
( )