题目内容
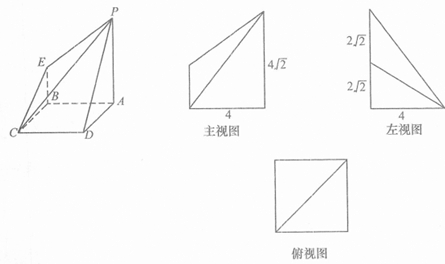
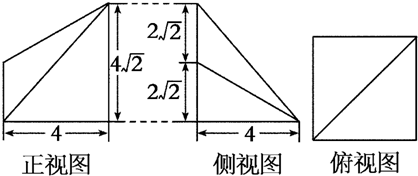 如图所示是一个几何体的直观图、正视图、俯视图和侧视图(尺寸如图所示).
如图所示是一个几何体的直观图、正视图、俯视图和侧视图(尺寸如图所示).(1)求四棱锥P-ABCD的体积;
(2)若G为BC上的动点,求证:AE⊥PG.
分析:(1)结合三视图,得到几何体及其相关棱长,求四棱锥P-ABCD的底面面积和高,即可求出VP-ABCD的体积.
(2)连BP,由已知中
=
=
,∠EBA与∠BAP均为直角,我们可以得到PB⊥AE,结合BC⊥AE,及线面垂直的判定定理,得到AE⊥面PBG,再由线面垂直的性质定理,即可得到答案.
(2)连BP,由已知中
| EB |
| AB |
| BA |
| PA |
| 1 | ||
|
解答: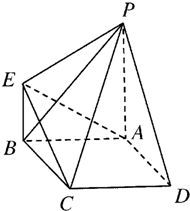 解:(1)由几何体的三视图可知,底面ABCD是边长为4的正方形,
解:(1)由几何体的三视图可知,底面ABCD是边长为4的正方形,
PA⊥平面ABCD,PA∥EB,且PA=4
,BE=2
,AB=AD=CD=CB=4,
∴VP-ABCD=
PA•S四边形ABCD=
×4
×4×4=
.
(2)连接BP,
∵
=
=
,∠EBA=∠BAP=90°,
∴∠PBA=∠BEA.
∴∠PBA+∠BAE=∠BEA+∠BAE=90°.
∴PB⊥AE.
又BC⊥平面APEB,
∴BC⊥AE.
∴AE⊥平面PBG.
∴AE⊥PG.
 解:(1)由几何体的三视图可知,底面ABCD是边长为4的正方形,
解:(1)由几何体的三视图可知,底面ABCD是边长为4的正方形,PA⊥平面ABCD,PA∥EB,且PA=4
| 2 |
| 2 |
∴VP-ABCD=
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
64
| ||
| 3 |
(2)连接BP,
∵
| EB |
| AB |
| BA |
| PA |
| 1 | ||
|
∴∠PBA=∠BEA.
∴∠PBA+∠BAE=∠BEA+∠BAE=90°.
∴PB⊥AE.
又BC⊥平面APEB,
∴BC⊥AE.
∴AE⊥平面PBG.
∴AE⊥PG.
点评:本题是中档题,考查直线与平面垂直的性质及几何体的体积的求法,考查计算能力.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案
相关题目
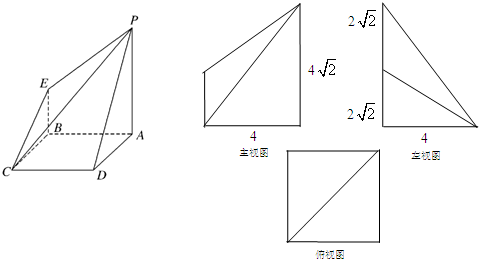
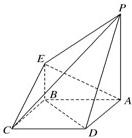 如图所示是一个几何体的直观图、正视图、俯视图、侧视图(其中正视图为直角梯形,俯视图为正方形,侧视图为直角三角形,尺寸如图所示).
如图所示是一个几何体的直观图、正视图、俯视图、侧视图(其中正视图为直角梯形,俯视图为正方形,侧视图为直角三角形,尺寸如图所示).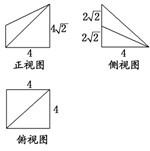
 如图所示是一个几何体的三视图(单位:cm),则这个几何体的表面积
如图所示是一个几何体的三视图(单位:cm),则这个几何体的表面积 如图所示是一个几何体的三视图,其侧视图是一个边长为a的等边三角形,俯视图是两个正三角形拼成的菱形,则该几何体的体积为
如图所示是一个几何体的三视图,其侧视图是一个边长为a的等边三角形,俯视图是两个正三角形拼成的菱形,则该几何体的体积为