题目内容
1．若函数f（x）=ax2+$\frac{1}{x}$，则下列结论正确的是（ ）| A． | ?a∈R，函数f（x）是奇函数 | B． | ?a∈R，函数f（x）是偶函数 | ||
| C． | ?a∈R，函数f（x）在（0，+∞）上是增函数 | D． | ?a∈R，函数f（x）在（0，+∞）上是减函数 |
分析 由题意可得当a=0时，f（x）=$\frac{1}{x}$，f（x）是奇函数，且函数f（x）在（0，+∞）上是减函数，排除A，B；再根据当a＜0，函数f（x）为减函数，故排除C，从而得出结论．
解答 解：对于函数f（x）=ax2+$\frac{1}{x}$，当a=0时，f（x）=$\frac{1}{x}$，此时，f（x）是奇函数，
且函数f（x）在（0，+∞）上是减函数；
当a≠0时，函数f（x）=ax2+$\frac{1}{x}$为非奇非偶函数，故排除A，B．
当a＜0，在（0，+∞）上，f′（x）=2ax-$\frac{1}{{x}^{2}}$＜0，函数f（x）为减函数，故排除C，
故选：D．
点评 本题主要考查函数的奇偶性、单调性的判断和证明，利用导数研究函数的单调性，属于基础题．
练习册系列答案
相关题目
11．已知抛物线x=$\frac{1}{4}$y2的焦点为F，过抛物线的准线l与x轴的交点M作抛物线的一条切线，切点为A，连接AF交抛物线于另一点B，则△MAB的面积为（ ）
| A． | 4 | B． | 6 | C． | 8 | D． | 12 |
9．已知函数f（x）=sin2x+acos2x（x∈R，a为∈R），若将其图象向右平移$\frac{π}{6}$个单位长度后，所得函数的一个对称中心为（$\frac{π}{2}$，0），则a的值为（ ）
| A． | $\sqrt{3}$ | B． | -1 | C． | 1 | D． | -$\frac{\sqrt{3}}{3}$ |
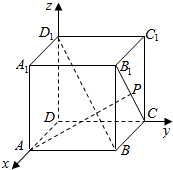如图所示，正方体ABCD-A1B1C1D1的棱长为1，以D为原点，以正方体的三条棱DA，DC，DD1所在的直线分别为x轴，y轴，z轴建立空间直角坐标系，若点P在正方体的侧面BCC1B1及其边界上运动，并且总是保持AP⊥BD1，则下列点P的坐标①（1，1，1），②（0，1，0），③（1，1，0），④（0，1，1），⑤（$\frac{1}{2}$，1，$\frac{1}{2}$）中正确的是①②⑤．
10．函数y=log5（x+1）的反函数是（ ）
| A． | y=5x+1 | B． | y=5x-1 | C． | y=-5x+1 | D． | y=5x-1 |
12．复数$\frac{2+i}{i}$（i是虚数单位）的虚部为（ ）
| A． | -2 | B． | -1 | C． | 1 | D． | 2 |