题目内容
13.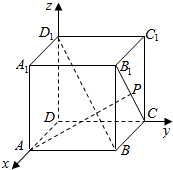 如图所示,正方体ABCD-A1B1C1D1的棱长为1,以D为原点,以正方体的三条棱DA,DC,DD1所在的直线分别为x轴,y轴,z轴建立空间直角坐标系,若点P在正方体的侧面BCC1B1及其边界上运动,并且总是保持AP⊥BD1,则下列点P的坐标①(1,1,1),②(0,1,0),③(1,1,0),④(0,1,1),⑤($\frac{1}{2}$,1,$\frac{1}{2}$)中正确的是①②⑤.
如图所示,正方体ABCD-A1B1C1D1的棱长为1,以D为原点,以正方体的三条棱DA,DC,DD1所在的直线分别为x轴,y轴,z轴建立空间直角坐标系,若点P在正方体的侧面BCC1B1及其边界上运动,并且总是保持AP⊥BD1,则下列点P的坐标①(1,1,1),②(0,1,0),③(1,1,0),④(0,1,1),⑤($\frac{1}{2}$,1,$\frac{1}{2}$)中正确的是①②⑤.
分析 根据空间坐标系,表示出点的坐标,设P(m,1,n),且(0≤m,n≤1),根据向量垂直得到m=n,即可判断答案.
解答 解:由题意可知,A(1,0,0),B(1,1,0),D1(0,0,1),
设P(m,1,n),且(0≤m,n≤1)
∴$\overrightarrow{AP}$=(m-1,1,n),$\overrightarrow{B{D}_{1}}$=(-1,-1,1),
∵AP⊥BD1,
∴$\overrightarrow{AP}$•$\overrightarrow{B{D}_{1}}$=1-m-1+n=n-m=0,
即m=n,
∴①(1,1,1),②(0,1,0),⑤($\frac{1}{2}$,1,$\frac{1}{2}$)满足条件,
故答案为:①②⑤.
点评 本题考查了空间向量的坐标运算和向量垂直的条件,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.9,a,b,243是等比数列,则a,b的值分别为( )
| A. | 27,81 | B. | 81,27 | C. | -27,81 | D. | 27,-81 |
1.若函数f(x)=ax2+$\frac{1}{x}$,则下列结论正确的是( )
| A. | ?a∈R,函数f(x)是奇函数 | B. | ?a∈R,函数f(x)是偶函数 | ||
| C. | ?a∈R,函数f(x)在(0,+∞)上是增函数 | D. | ?a∈R,函数f(x)在(0,+∞)上是减函数 |
5.一质点的运动方程为s(t)=2t2-1,则在时间段[1-△t,1+△t]内相应的平均速度为( )
| A. | 4 | B. | 2 | C. | 4+2△t | D. | 4-2△t |