题目内容
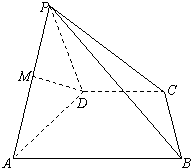 如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD,侧面PA⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为AP的中点.
如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD,侧面PA⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为AP的中点.(Ⅰ)求证:AD⊥PB;
(Ⅱ)求证:DM∥平面PCB;
(Ⅲ)求二面角A-BC-P的正切值.
考点:二面角的平面角及求法,直线与平面平行的判定
专题:空间位置关系与距离,空间角
分析:(Ⅰ)取AD的中点G,连结PG、GB、BD,由已知得PG⊥AD,△ABD是正三角形,BG⊥AD,从而AD⊥平面PGB,由此能证明AD⊥PB.
(Ⅱ)取PB的中点F,联结MF、CF,由已知得四边形CDFM是平行四边形,由此能证明DM∥平面PCB.
(Ⅲ)取BC的中点E,联结PE、GE,则∠PEC是二面角A-BC-P的平面角,由此能求出二面角A-BC-P的正切值.
(Ⅱ)取PB的中点F,联结MF、CF,由已知得四边形CDFM是平行四边形,由此能证明DM∥平面PCB.
(Ⅲ)取BC的中点E,联结PE、GE,则∠PEC是二面角A-BC-P的平面角,由此能求出二面角A-BC-P的正切值.
解答:
 (Ⅰ)证明:取AD的中点G,连结PG、GB、BD. …(1分)
(Ⅰ)证明:取AD的中点G,连结PG、GB、BD. …(1分)
∵PA=PD,∴PG⊥AD.…(2分)
∵AB=AD,且∠DAB=60°,
∴△ABD是正三角形,BG⊥AD.…(3分)
∴AD⊥平面PGB,∴AD⊥PB.…(4分)
(Ⅱ)证明:取PB的中点F,联结MF、CF,
∵M、F分别为PA、PB的中点,
∴MF∥AB,且MF=
AB.…(5分)
∵四边形ABCD是直角梯形,AB∥CD,且AB=2CD,
∴MF∥CD,且MF=CD.…(6分)
∴四边形CDFM是平行四边形,∴DM∥CF. …(8分)
∵CF?平面PCB,∴DM∥平面PCB. …(9分)
(Ⅲ)解:取BC的中点E,联结PE、GE,
∵四边形ABCD是直角梯形,且AB∥CD,
∴GE∥AB,GE⊥BC,∴BC⊥平面PEC,∴BC⊥PE,
∴∠PEC是二面角A-BC-P的平面角.…(11分)
设DC=a,则AB=AD=2a,
∵G、E分别为AD、BC中点,∴GE=
=
a.
∵G是等腰直角三角形PAD斜边的中点,∴PG=
AD=a.…(13分)
∴tan∠PEG=
,∴二面角A-BC-P的正切值为
.…(14分)
 (Ⅰ)证明:取AD的中点G,连结PG、GB、BD. …(1分)
(Ⅰ)证明:取AD的中点G,连结PG、GB、BD. …(1分)∵PA=PD,∴PG⊥AD.…(2分)
∵AB=AD,且∠DAB=60°,
∴△ABD是正三角形,BG⊥AD.…(3分)
∴AD⊥平面PGB,∴AD⊥PB.…(4分)
(Ⅱ)证明:取PB的中点F,联结MF、CF,
∵M、F分别为PA、PB的中点,
∴MF∥AB,且MF=
| 1 |
| 2 |
∵四边形ABCD是直角梯形,AB∥CD,且AB=2CD,
∴MF∥CD,且MF=CD.…(6分)
∴四边形CDFM是平行四边形,∴DM∥CF. …(8分)
∵CF?平面PCB,∴DM∥平面PCB. …(9分)
(Ⅲ)解:取BC的中点E,联结PE、GE,
∵四边形ABCD是直角梯形,且AB∥CD,
∴GE∥AB,GE⊥BC,∴BC⊥平面PEC,∴BC⊥PE,
∴∠PEC是二面角A-BC-P的平面角.…(11分)
设DC=a,则AB=AD=2a,
∵G、E分别为AD、BC中点,∴GE=
| AB+CD |
| 2 |
| 3 |
| 2 |
∵G是等腰直角三角形PAD斜边的中点,∴PG=
| 1 |
| 2 |
∴tan∠PEG=
| 2 |
| 3 |
| 2 |
| 3 |
点评:本题考查异面直线垂直的证明,考查直线与平面平行的证明,考查二面角的正切值的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
设双曲线C1,抛物线C2的焦点均在x轴上,C1的中心与C2的顶点均为原点,从每条曲线上至少取一个点,将其坐标记录如下:
则在C1和C2上点的个数分别是( )
| x | 1 |
|
| 2 | 3 | ||||||
| y | 2
|
| 2 | 4 | 2
|
| A、1,4 | B、2,3 |
| C、4,1 | D、3,3 |
函数f(x)=lnx-
的零点所在的大致区间是( )
| 2 |
| x |
| A、(1,2) | ||
| B、(2,3) | ||
C、(1,
| ||
| D、(e,+∞) |
下列各点中,不在方程x2-xy+2y+1=0表示的曲线上的点是( )
| A、(1,-2) |
| B、(-2,1) |
| C、(-3,-2) |
| D、(3,10) |
 如图是1,2两组各7名同学体重(单位:kg)数据的茎叶图,设1,2两组数据的平均数依次为
如图是1,2两组各7名同学体重(单位:kg)数据的茎叶图,设1,2两组数据的平均数依次为. |
| x1 |
. |
| x2 |
(注:标准差s=
| 1 |
| n |
(x1-
|
. |
| x |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
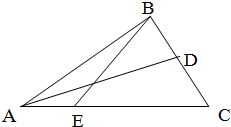 如图,在△ABC中,D是BC的中点,E是AC的三等分点,且EC=2AE,若
如图,在△ABC中,D是BC的中点,E是AC的三等分点,且EC=2AE,若