题目内容
设不等式|2x-1|＜1的解集为M．
（Ⅰ）求集合M；
（Ⅱ）若a，b∈M，求证：ab+1＞a+b．
（Ⅰ）求集合M；
（Ⅱ）若a，b∈M，求证：ab+1＞a+b．
考点：绝对值不等式的解法
专题：证明题,不等式的解法及应用
分析：（Ⅰ）由|2x-1|＜1得-1＜2x-1＜1，解之即可；
（Ⅱ）依题意，0＜a＜1，0＜b＜1，将所证不等式作差化积，利用不等式的性质判断即可证得结论．
（Ⅱ）依题意，0＜a＜1，0＜b＜1，将所证不等式作差化积，利用不等式的性质判断即可证得结论．
解答：
不等式选讲
解 （Ⅰ）由|2x-1|＜1得-1＜2x-1＜1，解得0＜x＜1．
所以M={x|0＜x＜1}．…（5分）
（Ⅱ）由（Ⅰ）和a，b∈M，可知0＜a＜1，0＜b＜1．
所以（ab+1）-（a+b）=（a-1）（b-1）＞0．
故ab+1＞a+b．…（10分）
解 （Ⅰ）由|2x-1|＜1得-1＜2x-1＜1，解得0＜x＜1．
所以M={x|0＜x＜1}．…（5分）
（Ⅱ）由（Ⅰ）和a，b∈M，可知0＜a＜1，0＜b＜1．
所以（ab+1）-（a+b）=（a-1）（b-1）＞0．
故ab+1＞a+b．…（10分）
点评：本题考查绝对值不等式的解法，考查不等式的证明，着重考查作差法的应用，属于中档题．
练习册系列答案
黄冈天天练口算题卡系列答案
相关题目
已知点A（3，4，0）和向量
=（1，-2，1），点B（0，m，n）在yOz平面上，使向量
∥
，则点B的坐标为（ ）
| a |
| AB |
| a |
| A、（0，-10，3） |
| B、（0，10，-3） |
| C、（0，-2，3） |
| D、（0，2，-3） |
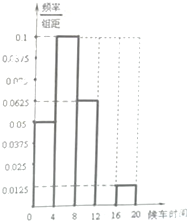常州公交公司为了调整302线路发车的时间间隔，在某站点对乘客进行了候车时间的调查，以下是候车时间的频率分布表和频率分布直方图．