题目内容
13.有以下四个命题:①动点M到两定点A,B的距离之比为常数λ(λ>0),则动点M的轨迹是圆;②当α变化时,方程x2+y2cosα=1表示的曲线不能是椭圆;③若椭圆$\frac{{x}^{2}}{5a}$+$\frac{{y}^{2}}{4{a}^{2}+1}$的焦点在x轴上,则它的离心率的取值范围是(0,$\frac{\sqrt{5}}{5}$];④已知抛物线y2=2px(p>0)上两点A(x1,y1),B(x2,y2),且$\overrightarrow{OA}$•$\overrightarrow{OB}$=0(O为原点),则y1•y2=-4p2.其中真命题是③④(填上你认为是真命题的所有序号)分析 对于①,通过建立坐标系,求出动点的轨迹方程判断;对于②,举例加以说明;对于③,据椭圆$\frac{{x}^{2}}{5a}$+$\frac{{y}^{2}}{4{a}^{2}+1}$=1的焦点在x轴上,确定a的范围,表示出椭圆的离心率,利用基本不等式,可得结论;对于④,利用直线和抛物线的位置关系判断.
解答 解:对于①,以AB所在的直线为x轴,AB的中垂线为y轴建立坐标系,设M(x,y),A(-a,0),B(a,0),则有$\frac{\sqrt{(x+a)^{2}+{y}^{2}}}{\sqrt{(x-a)^{2}+{y}^{2}}}=λ$,
化简得(1-λ2)x2+(1-λ2)y2+(2a+2aλ2)x+a2-a2λ2=0,当λ=1时,方程为x=0,不是圆.故①错误;
对于②,当0°<α<90°时,0<cosα<1,方程x2+y2cosα=1表示中心在原点,焦点在y轴上的椭圆.故②错误;
对于③,若椭圆$\frac{{x}^{2}}{5a}$+$\frac{{y}^{2}}{4{a}^{2}+1}$的焦点在x轴上,∴5a>4a2+1,
∴$\frac{1}{4}$<a<1.
∵椭圆的离心率为$\sqrt{\frac{5a-4{a}^{2}-1}{5a}}$=$\sqrt{1-\frac{1}{5}(4a+\frac{1}{a})}$≤$\sqrt{1-\frac{1}{5}•2\sqrt{4a•\frac{1}{4a}}}$=$\frac{\sqrt{5}}{5}$(当且仅当4a=$\frac{1}{a}$,即a=$\frac{1}{2}$时取等号),
∴椭圆的离心率的取值范围为(0,$\frac{\sqrt{5}}{5}$].故③正确;
对于④,A(x1,y1),B(x2,y2)是抛物线y2=2px(p>0)上的两点,并且满足$\overrightarrow{OA}$•$\overrightarrow{OB}$=0,
∴kOA•kOB=-1,∴x1x2+y1y2=0,则$\frac{({y}_{1}{y}_{2})^{2}}{4{p}^{2}}+{y}_{1}{y}_{2}=0$,解得y1y2=-4p2,故④正确.
∴正确命题的序号是③④.
故答案为:③④.
点评 本题考查命题的真假判断与应用,着重考查圆锥曲线的基本性质,熟练掌握圆锥曲线的性质是解答该题的关键,是中档题.

 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案| A. | f(1)<c | B. | f(1)>c | C. | f(2)<c | D. | f(2)>c |
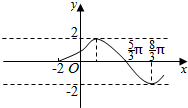
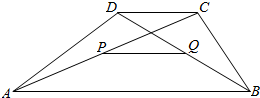 设P,Q分别是梯形ABCD的对角线AC与BD的中点
设P,Q分别是梯形ABCD的对角线AC与BD的中点 .
. 在点
在点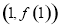 处的切线方程为
处的切线方程为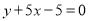 ,求函数
,求函数 是函数
是函数 ,求
,求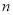 的值;
的值; 时,函数
时,函数 ,且
,且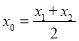 ,求证:
,求证: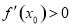 .
.