题目内容
已知x,y都是正实数,且x+y>1.用反证法证明:
>
或
>
中至少有一个成立.
| y |
| 1+x |
| 1 |
| 3 |
| x |
| 1+y |
| 1 |
| 3 |
考点:反证法与放缩法
专题:证明题,反证法,不等式的解法及应用
分析:假设
>
与
>
都不成立,即
≤
且
≤
,根据x,y都是正数可得x+y≤1,这与已知x+y>1矛盾,故假设不成立.
| y |
| 1+x |
| 1 |
| 3 |
| x |
| 1+y |
| 1 |
| 3 |
| y |
| 1+x |
| 1 |
| 3 |
| x |
| 1+y |
| 1 |
| 3 |
解答:
证明:假设
>
与
>
都不成立,即
≤
且
≤
,…(2分)
∵x,y都是正数,∴1+x≥3y,1+y≥3x,…(5分)
∴1+x+1+y≥3x+3y,…(8分)
∴x+y≤1…(10分)
这与已知x+y>1矛盾…(12分)
∴假设不成立,即
>
或
>
中至少有一个成立…(14分)
| y |
| 1+x |
| 1 |
| 3 |
| x |
| 1+y |
| 1 |
| 3 |
| y |
| 1+x |
| 1 |
| 3 |
| x |
| 1+y |
| 1 |
| 3 |
∵x,y都是正数,∴1+x≥3y,1+y≥3x,…(5分)
∴1+x+1+y≥3x+3y,…(8分)
∴x+y≤1…(10分)
这与已知x+y>1矛盾…(12分)
∴假设不成立,即
| y |
| 1+x |
| 1 |
| 3 |
| x |
| 1+y |
| 1 |
| 3 |
点评:本题主要考查用反证法证明数学命题,应先假设要证的命题的否定成立,推出矛盾,是解题的关键和难点,属于中档题.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
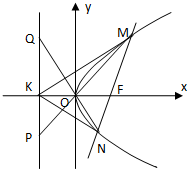 如图,已知抛物线y2=4x的焦点为F,过F的直线交抛物线于M、N两点,其准线l与x轴交于K点.
如图,已知抛物线y2=4x的焦点为F,过F的直线交抛物线于M、N两点,其准线l与x轴交于K点.