题目内容
1.复数z=(2a2-a-1)+(a-1)i,a∈R.(1)若z为实数,求a的值;
(2)若z为纯虚数,求a的值;
(3)若z=9-3i,求a的值.
分析 (1)根据虚数部分是0,求出a的值即可;(2)根据纯虚数的定义求a即可;(3)根据系数相等得到关于a的方程组,解出即可.
解答 解:(1)若z为实数,则a-1=0,得a=1. (2分)
(2)若z为纯虚数,则$\left\{{\begin{array}{l}{2{a^2}-a-1=0}\\{a-1≠0}\end{array}}\right.$,解得$a=-\frac{1}{2}$.(6分)
(3)若z=9-3i,则$\left\{{\begin{array}{l}{2{a^2}-a-1=9}\\{a-1=-3}\end{array}}\right.$,解得a=-2. (10分)
点评 本题考查了复数的基本概念,熟练掌握定义是解题的关键,本题是一道基础题.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
6.已知向量$\overrightarrow a$=(m,0}),向量$\overrightarrow b,\overrightarrow c$满足$\overrightarrow a$⊥$\overrightarrow{b$,$\overrightarrow c$-$\overrightarrow a$=2$\overrightarrow b$,且|$\overrightarrow c$|=$\sqrt{10}$,若$\overrightarrow c$与$\overrightarrow a$+$\overrightarrow b$夹角的余弦值为$\frac{{3\sqrt{10}}}{10}$,则|$\overrightarrow b$|=( )
| A. | $\sqrt{2}$ | B. | $\frac{5}{4}$ | C. | $\frac{5}{4}$或2 | D. | $\sqrt{2}$或$\frac{{\sqrt{5}}}{2}$ |
10.在等差数列{an}中,已知an=11-2n,则使前n项和Sn最大的n值为( )
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
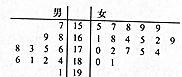 某初中对初二年级的学生进行体质测试,已知初二一班共有学生30人,测试立定跳远的成绩用茎叶图表示如下(单位:cm):
某初中对初二年级的学生进行体质测试,已知初二一班共有学生30人,测试立定跳远的成绩用茎叶图表示如下(单位:cm): 空气质量指数(Air Quality Index,简称AQI)是定量描述空气质量状况的质量状况的指数,空气质量按照AQI大小分为六级,0~50为优;51~100为良101-150为轻度污染;151-200为中度污染;201~300为重度污染;>300为严重污染.
空气质量指数(Air Quality Index,简称AQI)是定量描述空气质量状况的质量状况的指数,空气质量按照AQI大小分为六级,0~50为优;51~100为良101-150为轻度污染;151-200为中度污染;201~300为重度污染;>300为严重污染. 如图,在长方体ABCD-A1B1C1D1中,已知AD=AA1=1,AB=2,点E是AB的中点.
如图,在长方体ABCD-A1B1C1D1中,已知AD=AA1=1,AB=2,点E是AB的中点.