题目内容
12.已知x,y满足(x-2)2+(y-3)2=1,则z=x2+y2的最小值为14-2$\sqrt{13}$.分析 根据圆的圆心和半径,以及z=x2+y2的表示圆上的点到原点的距离的平方,求得它的最小值.
解答 解:方程(x-2)2+(y-3)2=1表示以(2,3)为圆心、半径等于1的圆,
故圆心到原点的距离为$\sqrt{4+9}$=$\sqrt{13}$,
z=x2+y2的表示圆上的点到原点的距离的平方,故它的最小值为${(\sqrt{13}-1)}^{2}$=14-2$\sqrt{13}$,
故答案为:14-2$\sqrt{13}$.
点评 本题主要考查圆的标准方程,点和圆的位置关系,属于基础题.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
12.一个物体的运动方程为s=1-t+t2其中s的单位是米,t的单位是秒,那么物体在3秒末的瞬时速度是( )
| A. | 7米/秒 | B. | 6米/秒 | C. | 5米/秒 | D. | 8米/秒 |
4.若直线l1:ax+2y+6=0与直线${l_2}:x+(a-1)y+{a^2}-1=0$平行,则a=( )
| A. | .2或-1 | B. | .2 | C. | -1 | D. | 以上都不对 |
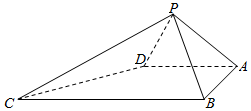 如图,四棱锥P-ABCD中,∠ABC=∠BAD=90°,BC=2AD,△PAB与△PAD都是等边三角形.
如图,四棱锥P-ABCD中,∠ABC=∠BAD=90°,BC=2AD,△PAB与△PAD都是等边三角形.