题目内容
【题目】如图所示,四棱锥P﹣ABCD中,平面PAD⊥平面ABCD,PA=PD![]() ,四边形ABCD为等腰梯形,BC∥AD,BC=CD
,四边形ABCD为等腰梯形,BC∥AD,BC=CD![]() AD=1,E为PA的中点.
AD=1,E为PA的中点.
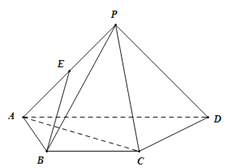
(1)求证:EB∥平面PCD;
(2)求平面PAC与平面PCD所成角的余弦值.
【答案】(1)证明见解析 (2) ![]() .
.
【解析】
(1)取AD中点F,连结EF、BF,推导出BF∥CD,EF∥PD,从而平面BEF∥平面PCD,由此能证明EB∥平面PCD.
(2)连结PF,则PF⊥平面ABCD,四边形BCDF是边长为1的菱形,△ABF是边长为1的等边三角形,以F为原点,在平面ABCD中过F作AD的垂线为x轴,FD为y轴,FP为z轴,建立空间直角坐标系,利用向量法能求出平面PAC与平面PCD所成角的余弦值.
(1)证明:取AD中点F,连结EF、BF,
∵BC∥AD,BC=CD![]() AD=1,E为PA的中点,
AD=1,E为PA的中点,
∴BF∥CD,EF∥PD,
∵BF∩EF=F,CD∩PD=D,
∴平面BEF∥平面PCD,
∵EB平面BEF,∴EB∥平面PCD.
(2)解:连结PF,∵四棱锥P﹣ABCD中,平面PAD⊥平面ABCD,PA=PD![]() ,
,
四边形ABCD为等腰梯形,BC∥AD,BC=CD![]() AD=1,E为PA的中点.
AD=1,E为PA的中点.
∴PF⊥平面ABCD,四边形BCDF是边长为1的菱形,△ABF是边长为1的等边三角形,
以F为原点,在平面ABCD中过F作AD的垂线为x轴,FD为y轴,FP为z轴,建立空间直角坐标系,
则P(0,0,1),A(0,﹣1,0),C(![]() ,
,![]() ,0),D(0,1,0),
,0),D(0,1,0),
![]() (0,﹣1,﹣1),
(0,﹣1,﹣1),![]() (
(![]() ,
,![]() ,﹣1),
,﹣1),![]() (0,1,﹣1),
(0,1,﹣1),
设平面PAC的法向量![]() (x,y,z),
(x,y,z),
则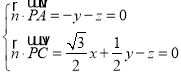 ,取y=1,得
,取y=1,得![]() (
(![]() ,1,﹣1),
,1,﹣1),
设平面PCD的法向量![]() (x,y,z),
(x,y,z),
则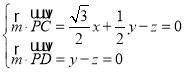 ,取y=1,得
,取y=1,得![]() (
(![]() ,1,1),
,1,1),
设平面PAC与平面PCD所成角为θ,
则cosθ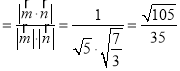 .
.
∴平面PAC与平面PCD所成角的余弦值为![]() .
.