题目内容
【题目】已知过原点的动直线l与圆![]() 相交于不同的两点A,B.
相交于不同的两点A,B.
(1)求线段AB的中点M的轨迹C的方程;
(2)是否存在实数k,使得直线L:y=k(x﹣4)与曲线C只有一个交点?若存在,求出k的取值范围;若不存在,说明理由.
【答案】(1)![]() (2)
(2)
【解析】试题分析:(Ⅰ)利用圆的几何性质,总有![]() ,根据斜率公式得到轨迹方程;(Ⅱ)做出曲线
,根据斜率公式得到轨迹方程;(Ⅱ)做出曲线![]() 的图象,
的图象, ![]() 恒过点
恒过点![]() ,利用数形结合,可知斜率的变化范围.
,利用数形结合,可知斜率的变化范围.
试题解析:(Ⅰ)设![]() ,则
,则![]() ,
,
当直线![]() 的斜率不为0时,由
的斜率不为0时,由![]() 得
得![]() ,即
,即![]()
当直线![]() 的斜率为0时,
的斜率为0时,![]() 也适合上述方程
也适合上述方程
∴ 线段![]() 的中点
的中点![]() 的轨迹的方程为
的轨迹的方程为![]() ;
;
(Ⅱ)由(Ⅰ)知点![]() 的轨迹是以
的轨迹是以![]() 为圆心
为圆心![]() 为半径的部分圆弧
为半径的部分圆弧![]() (如下图所示,不包括两端点),且
(如下图所示,不包括两端点),且 ,
, ,又直线
,又直线![]() :
: ![]() 过定点
过定点![]() ,当直线
,当直线![]() 与圆
与圆![]() 相切时,由
相切时,由 得
得![]() ,又
,又 ,结合上图可知当
,结合上图可知当 时,直线
时,直线![]() :
: ![]() 曲线
曲线![]() 只有一个交点.
只有一个交点.


 名校课堂系列答案
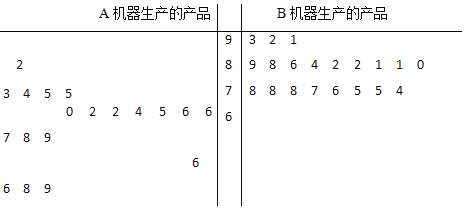
名校课堂系列答案【题目】某工厂有两台不同机器A和B生产同一种产品各10万件,现从各自生产的产品中分别随机抽取20件,进行品质鉴定,鉴定成绩的茎叶图如图所示:
该产品的质量评价标准规定:鉴定成绩达到![]() 的产品,质量等级为优秀;鉴定成绩达到
的产品,质量等级为优秀;鉴定成绩达到![]() 的产品,质量等级为良好;鉴定成绩达到
的产品,质量等级为良好;鉴定成绩达到![]() 的产品,质量等级为合格
的产品,质量等级为合格![]() 将这组数据的频率视为整批产品的概率.
将这组数据的频率视为整批产品的概率.
![]() Ⅰ
Ⅰ![]() 从等级为优秀的样本中随机抽取两件,记X为来自B机器生产的产品数量,写出X的分布列,并求X的数学期望;
从等级为优秀的样本中随机抽取两件,记X为来自B机器生产的产品数量,写出X的分布列,并求X的数学期望;
![]() Ⅱ
Ⅱ![]() 完成下列
完成下列![]() 列联表,以产品等级是否达到良好以上
列联表,以产品等级是否达到良好以上![]() 含良好
含良好![]() 为判断依据,判断能不能在误差不超过
为判断依据,判断能不能在误差不超过![]() 的情况下,认为B机器生产的产品比A机器生产的产品好;
的情况下,认为B机器生产的产品比A机器生产的产品好;
A生产的产品 | B生产的产品 | 合计 | |
良好以上 | |||
合格 | |||
合计 |
![]() 已知优秀等级产品的利润为12元
已知优秀等级产品的利润为12元![]() 件,良好等级产品的利润为10元
件,良好等级产品的利润为10元![]() 件,合格等级产品的利润为5元
件,合格等级产品的利润为5元![]() 件,A机器每生产10万件的成本为20万元,B机器每生产10万件的成本为30万元;该工厂决定:按样本数据测算,两种机器分别生产10万件产品,若收益之差达到5万元以上,则淘汰收益低的机器,若收益之差不超过5万元,则仍然保留原来的两台机器
件,A机器每生产10万件的成本为20万元,B机器每生产10万件的成本为30万元;该工厂决定:按样本数据测算,两种机器分别生产10万件产品,若收益之差达到5万元以上,则淘汰收益低的机器,若收益之差不超过5万元,则仍然保留原来的两台机器![]() 你认为该工厂会仍然保留原来的两台机器吗?
你认为该工厂会仍然保留原来的两台机器吗?
附:![]() 独立性检验计算公式:
独立性检验计算公式:![]() .
.
![]() 临界值表:
临界值表:
|
|
|
|
|
|
k |
|
|
|
|
|
