Question

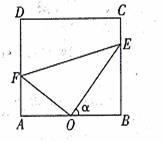
    学校生活区内建有一块矩形休闲区域ABCD，AB=100米，BC=50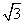米，为了便于同学们平时休闲散步，学校后勤部门将在这块区域内铺设三条小路OE、EF和OF，考虑到学校整体规划，要求O是AB的中点，点E在边BC上，点F在边AD上，且OE⊥OF,如图所示．

   （1）设∠BOE=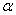，试将△OEF的周长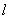表示成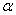的函数关系式，并求出此函数的定义域；

   （2）经核算，三条路每米铺设费用均为800元，试问如何设计才能使铺路的总费用最低？并求出最低总费用． 

Answer 1

 解：⑴在Rt△BOE中,,    ……………………………1分

在Rt△AOF中,     ……………………………2分

在Rt△OEF中,, ……………………………3分

所以    ……………………………5分

当点F在点D时,角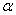最小,;    当点E在点C时,角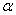最大,

函数的定义域为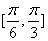   ………………………………………………………7分

⑵ 设,

则      …………9分

                         ……………………………10分

                  ……………………………11分

答: 当时,,总费用最低为元     ……