题目内容
已知椭圆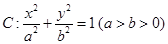 经过点
经过点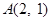 ,离心率为
,离心率为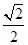 ,过点
,过点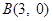 的直线
的直线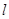 与椭圆
与椭圆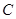 交于不同的两点
交于不同的两点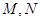 .
.
(1)求椭圆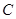 的方程;
的方程;
(2)求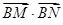 的取值范围.
的取值范围.
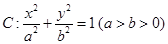 经过点
经过点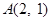 ,离心率为
,离心率为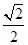 ,过点
,过点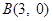 的直线
的直线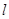 与椭圆
与椭圆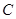 交于不同的两点
交于不同的两点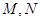 .
.(1)求椭圆
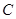 的方程;
的方程;(2)求
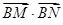 的取值范围.
的取值范围.(1) ;(2)
;(2)
 ;(2)
;(2)
试题分析:(1)由离心率为
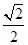 ,得
,得 ,再根据椭圆C过点
,再根据椭圆C过点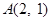 ,代入得
,代入得 ,联立之可求得
,联立之可求得 的值,进而写出椭圆方程;(2)考察直线和椭圆的位置关系,一般要将直线方程和椭圆方程联立,得关于某一变量的一元二次方程,设交点,然后利用韦达定理达到设而不求的目的,同时要注意
的值,进而写出椭圆方程;(2)考察直线和椭圆的位置关系,一般要将直线方程和椭圆方程联立,得关于某一变量的一元二次方程,设交点,然后利用韦达定理达到设而不求的目的,同时要注意 的隐含条件,该题设直线方程为
的隐含条件,该题设直线方程为 ,代入椭圆方程得
,代入椭圆方程得 ,则
,则 >0,得
>0,得 的范围,设交点
的范围,设交点
 ,
,
 ,将
,将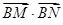 表示为
表示为 ,然后利用韦达定理将其表示为
,然后利用韦达定理将其表示为 的式子,进而可以看成是自变量为
的式子,进而可以看成是自变量为 的函数
的函数 ,求其值域即可.
,求其值域即可.试题解析:(1)由题意得
 解得
解得 ,
, .
. 椭圆
椭圆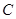 的方程为
的方程为 .
.(2)由题意显然直线
 的斜率存在,设直线
的斜率存在,设直线 的方程为
的方程为 ,
,由
 得
得 .
.  直线
直线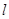 与椭圆
与椭圆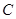 交于不同的两点
交于不同的两点 ,
, ,
,
 ,解得
,解得 .设
.设 ,
, 的坐标分别为
的坐标分别为 ,
, ,则
,则 ,
, ,
, ,
, .
.


 .
. ,
, .
. 的取值范围为
的取值范围为 .
. 
练习册系列答案
相关题目
 ·
· 的值;
的值; 的中心在坐标原点,边
的中心在坐标原点,边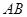 与
与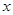 轴平行,
轴平行, =6.
=6.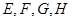 分别是矩形四条边的中点,
分别是矩形四条边的中点,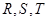 是线段
是线段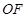 的四等分点,
的四等分点,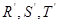 是线段
是线段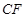 的四等分点.设直线
的四等分点.设直线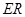 与
与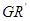 ,
,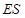 与
与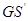 ,
,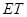 与
与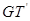 的交点依次为
的交点依次为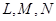 .
.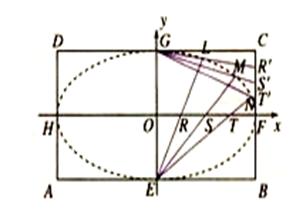
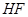 为长轴,以
为长轴,以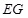 为短轴的椭圆Q的方程;
为短轴的椭圆Q的方程;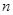 (
(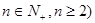 等分点从左向右依次为
等分点从左向右依次为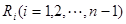 ,线段
,线段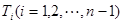 ,那么直线
,那么直线 与哪条直线的交点一定在椭圆Q上?(写出结果即可,此问不要求证明)
与哪条直线的交点一定在椭圆Q上?(写出结果即可,此问不要求证明)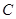 :
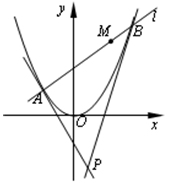
: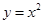 .过点
.过点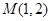 的直线
的直线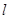 交
交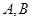 两点.抛物线
两点.抛物线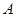 处的切线与在点
处的切线与在点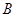 处的切线交于点
处的切线交于点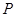 .
.
 ;
;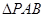 面积的最小值.
面积的最小值.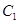 :
: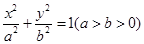 的左、右焦点分别是
的左、右焦点分别是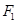 、
、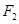 ,下顶点为
,下顶点为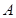 ,线段
,线段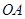 的中点为
的中点为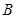 (
(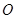 为坐标原点),如图.若抛物线
为坐标原点),如图.若抛物线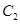 :
: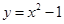 与
与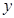 轴的交点为
轴的交点为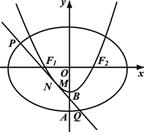
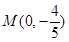 ,
, 为抛物线
为抛物线 、
、 两点,求
两点,求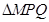 面积的最大值.
面积的最大值.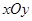 中,已知椭圆
中,已知椭圆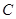 :
: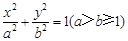 的离心率
的离心率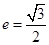 ,且椭圆C上一点
,且椭圆C上一点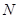 到点Q
到点Q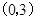 的距离最大值为4,过点
的距离最大值为4,过点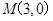 的直线交椭圆
的直线交椭圆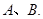
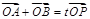 (O为坐标原点),当
(O为坐标原点),当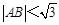 时,求实数
时,求实数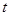 的取值范围.
的取值范围.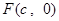 是椭圆
是椭圆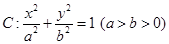 的右焦点,圆
的右焦点,圆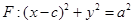 与
与 轴交于
轴交于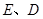 两点,
两点,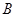 是椭圆
是椭圆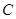 与圆
与圆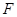 的一个交点,且
的一个交点,且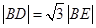
 与
与 ,且
,且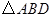 的面积为
的面积为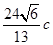 ,求椭圆
,求椭圆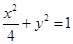 的左焦点作互相垂直的两条直线,分别交椭圆于
的左焦点作互相垂直的两条直线,分别交椭圆于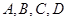 四点,则四边形
四点,则四边形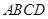 面积的最大值与最小值之差为( )
面积的最大值与最小值之差为( )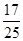
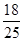
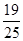
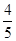
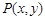 到两条坐标轴的距离之和等于它到点
到两条坐标轴的距离之和等于它到点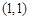 的距离,记点
的距离,记点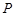 的轨迹为曲线
的轨迹为曲线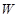 .
. 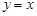 对称;
对称; 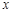 轴非负半轴,
轴非负半轴,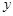 轴非负半轴围成的封闭图形的面积小于
轴非负半轴围成的封闭图形的面积小于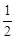 ;
;