题目内容
在平面直角坐标系 中,已知椭圆
中,已知椭圆 :
: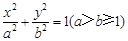 的离心率
的离心率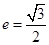 ,且椭圆C上一点
,且椭圆C上一点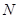 到点Q
到点Q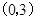 的距离最大值为4,过点
的距离最大值为4,过点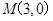 的直线交椭圆
的直线交椭圆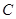 于点
于点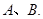
(Ⅰ)求椭圆C的方程;
(Ⅱ)设P为椭圆上一点,且满足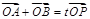 (O为坐标原点),当
(O为坐标原点),当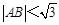 时,求实数
时,求实数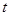 的取值范围.
的取值范围.
 中,已知椭圆
中,已知椭圆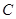 :
: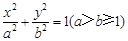 的离心率
的离心率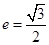 ,且椭圆C上一点
,且椭圆C上一点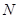 到点Q
到点Q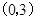 的距离最大值为4,过点
的距离最大值为4,过点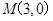 的直线交椭圆
的直线交椭圆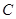 于点
于点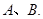
(Ⅰ)求椭圆C的方程;
(Ⅱ)设P为椭圆上一点,且满足
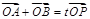 (O为坐标原点),当
(O为坐标原点),当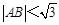 时,求实数
时,求实数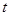 的取值范围.
的取值范围.(1)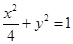 ;(2)
;(2)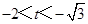 或
或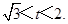
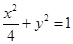 ;(2)
;(2)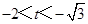 或
或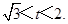
试题分析:本题主要考查椭圆的标准方程和几何性质、直线的方程、平面内两点间距离公式等基础知识,考查用代数方法研究圆锥曲线的性质以及数形结合的数学思想方法,考查运算求解能力、综合分析和解决问题的能力.第一问,先利用离心率列出表达式找到
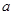 与
与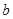 的关系,又因为椭圆上的
的关系,又因为椭圆上的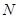 点到点
点到点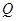 的距离最大值为4,利用两点间距离公式列出表达式,因为
的距离最大值为4,利用两点间距离公式列出表达式,因为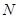 在椭圆上,所以
在椭圆上,所以 ,代入表达式,利用配方 法求最大值,从而求出
,代入表达式,利用配方 法求最大值,从而求出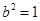 ,所以
,所以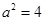 ,所以得到椭圆的标准方程;第二问,先设
,所以得到椭圆的标准方程;第二问,先设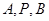 点坐标,由题意设出直线
点坐标,由题意设出直线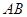 方程,因为直线与椭圆相交,列出方程组,消参韦达定理得到两根之和、两根之积,用坐标表示
方程,因为直线与椭圆相交,列出方程组,消参韦达定理得到两根之和、两根之积,用坐标表示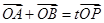 得出
得出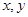 ,由于点
,由于点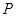 在椭圆上,得到一个表达式,再由
在椭圆上,得到一个表达式,再由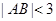 ,得到一个表达式,2个表达式联立,得到
,得到一个表达式,2个表达式联立,得到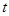 的取值范围.
的取值范围.试题解析:(Ⅰ)∵
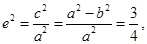 ∴
∴ (1分)
(1分)则椭圆方程为
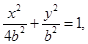 即
即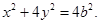
设
 则
则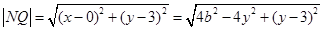
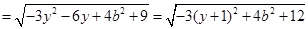
当
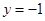 时,
时,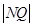 有最大值为
有最大值为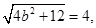
解得
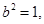 ∴
∴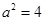 ,椭圆方程是
,椭圆方程是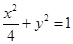 (4分)
(4分)(Ⅱ)设
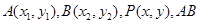 方程为
方程为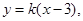
由
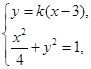 整理得
整理得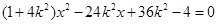 .
.由
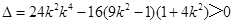 ,得
,得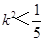 .
.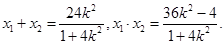 (6分)
(6分)∴
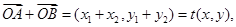 则
则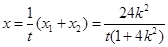 ,
,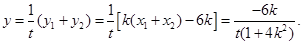
由点P在椭圆上,得
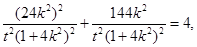 化简得
化简得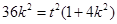 ① (8分)
① (8分)又由
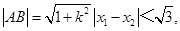 即
即 将
将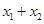 ,
,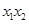 代入得
代入得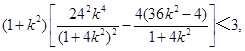 化简,得
化简,得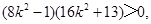
则
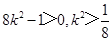 , ∴
, ∴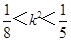 ② (10分)
② (10分)由①,得
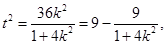
联立②,解得
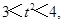 ∴
∴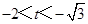 或
或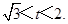 (12分)
(12分)
练习册系列答案
相关题目
 ,焦点在
,焦点在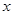 轴上的抛物线过点
轴上的抛物线过点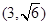 .
.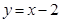 交于
交于 、
、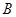 两点,求证:
两点,求证: .
.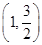 、
、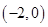 .记其上顶点为
.记其上顶点为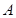 ,右顶点为
,右顶点为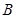 .
.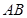 上,且与坐标轴相切于椭圆焦点的圆的方程;
上,且与坐标轴相切于椭圆焦点的圆的方程;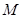 ,使
,使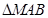 的面积最大.
的面积最大. 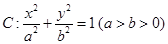 经过点
经过点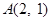 ,离心率为
,离心率为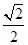 ,过点
,过点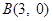 的直线
的直线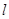 与椭圆
与椭圆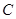 交于不同的两点
交于不同的两点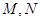 .
.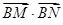 的取值范围.
的取值范围.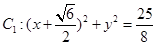 ,圆
,圆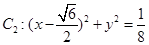 ,动圆
,动圆 与已知两圆都外切.
与已知两圆都外切. 的方程;
的方程;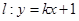 与点
与点 、
、 ,
, 的中垂线与
的中垂线与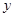 轴交于点
轴交于点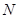 ,求点
,求点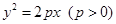 与直线
与直线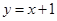 相切,
相切,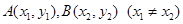 是抛物线上两个动点,
是抛物线上两个动点,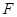 为抛物线的焦点,
为抛物线的焦点,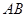 的垂直平分线
的垂直平分线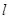 与
与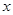 轴交于点
轴交于点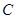 ,且
,且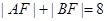 .
.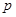 的值;
的值;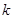 的取值范围.
的取值范围.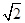 ,则P="__________" .
,则P="__________" .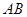 的两个端点在抛物线
的两个端点在抛物线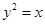 上滑动,则线段
上滑动,则线段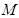 到
到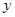 轴距离的最小值是
轴距离的最小值是 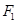 、
、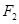 为双曲线C:
为双曲线C: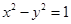 的左、右焦点,点P在C上,
的左、右焦点,点P在C上,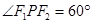 ,则
,则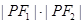 = ;
= ;