题目内容
已知n是大于1的自然数,求证:(1+
)(1+
)(1+
)…(1+
)＞
.
证明：假设n=k(k≥2)时,原不等式成立,即(1+)(1+)(1+)…(1+)＞2k+1.
则当n=k+1时,左边=(1+
)(1+
)(1+
)…(1+
)·(1+
)＞
·(1+
)= 
(
).
现在关键是证
,直接证较繁,下面用分析法证之.
欲证
,即证
,只需证2k+1+
+2＞2k+3,即证
＞0.
这显然是成立的,故当n=k+1时,原不等式成立.
综上,知n是大于1的自然数时,原不等式成立.
练习册系列答案
阅读快车系列答案
相关题目
＋
＋…＋
)(n≥2)．
)(1＋
)…(1＋
)＜e3(其中e为自然对数的底数)．
（
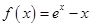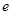是自然对数的底数）
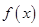的最小值；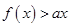
的解集为P, 若
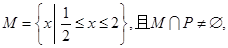求实数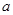
的取值范围；
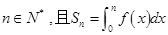，是否存在等差数列
和首项为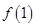
公比大于0的等比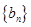数列
，使数列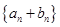
的前n项和等于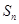
）（n≥2）．
）（1+
）…（1+
）＜e3（其中e为自然对数的底数）．