题目内容
已知函数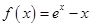 (
(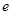 是自然对数的底数)
是自然对数的底数)
(1)求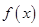 的最小值;
的最小值;
(2)不等式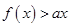 的解集为P, 若
的解集为P, 若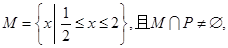 求实数
求实数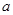 的取值范围;
的取值范围;
(3)已知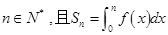 ,是否存在等差数列
,是否存在等差数列 和首项为
和首项为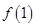 公比大于0的等比数列
公比大于0的等比数列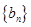 ,使数列
,使数列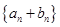 的前n项和等于
的前n项和等于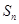
【答案】
(Ⅰ)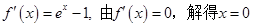
当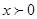 时,
时,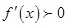 ;
当
;
当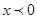 时,
时,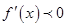
故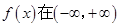 连续,故
连续,故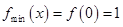 ————3分
————3分
(Ⅱ)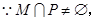 即不等式
即不等式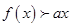 在区间
在区间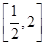 有解
有解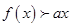 可化为
可化为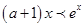 ,
,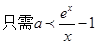 在区间
在区间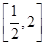 有解————4分
有解————4分
令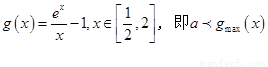 ————5分
————5分
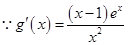 故
故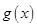 在区间
在区间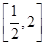 递减,在区间
递减,在区间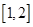 递增
递增
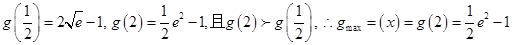 所以,实数a的取值范围为
所以,实数a的取值范围为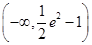 —————8分
—————8分
(Ⅲ)设存在公差为d首项等于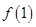 的等差数列
的等差数列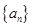 和公比q大于0的等比数列
和公比q大于0的等比数列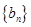 ,使得数列
,使得数列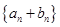 的前n项和等于
的前n项和等于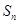
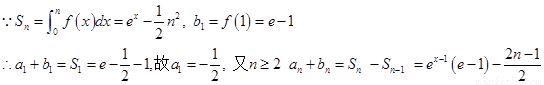 故
故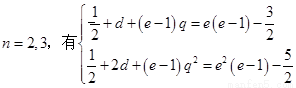
即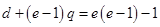 ①,
①, 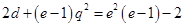 ②
②
②-①×2得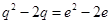 ,
, 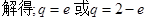 (舍去)
(舍去)
故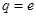 ,
,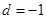 ,此时,
,此时,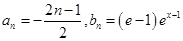 数列
数列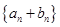 的的前n项和等于
的的前n项和等于
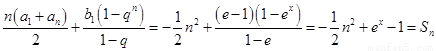
故存在满足题意的等差数列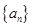 金额等比数列
金额等比数列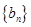 ,
,
使得数列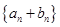 的前n项和等于
的前n项和等于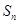
【解析】略

练习册系列答案
相关题目
 (
( 是自然对数的底数).
是自然对数的底数). 在
在 处的切线也是抛物线
处的切线也是抛物线 的切线,求
的切线,求 的值;
的值; 时,是否存在
时,是否存在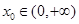 ,使曲线
,使曲线 在点
在点 处的切线斜率与
处的切线斜率与 在
在 上的最小值相等?若存在,求符合条件的
上的最小值相等?若存在,求符合条件的 的个数;若不存在,请说明理由.
的个数;若不存在,请说明理由.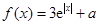 (
( …是自然对数的底数)的最小值为
…是自然对数的底数)的最小值为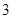 .
.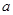 的值;
的值;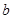
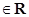 且
且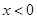 ,试解关于
,试解关于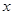 的不等式
的不等式 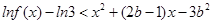 ;
;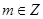 且
且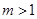 .若存在实数
.若存在实数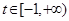 ,使得对任意的
,使得对任意的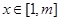 ,都有
,都有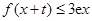 ,试求
,试求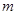 的最大值.
的最大值.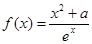
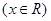 (
(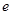 是自然对数的底数,
是自然对数的底数,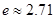 ).
).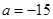 时,求
时,求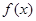 的单调区间;
的单调区间;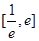 上是增函数,求实数
上是增函数,求实数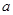 的取值范围;
的取值范围;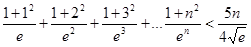 对一切
对一切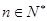 恒成立.
恒成立.
 (
(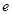 是自然对数的底数,
是自然对数的底数,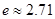 ).
).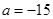 时,求
时,求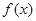 的单调区间;
的单调区间;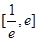 上是增函数,求实数
上是增函数,求实数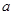 的取值范围;
的取值范围;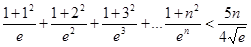 对一切
对一切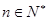 恒成立.
恒成立.