Question

(16)如图，函数y=2sin(πx+φ)，x∈R(其中0≤φ≤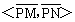)的图象与y轴交于点(0，1)．

(Ⅰ)求φ的值；

(Ⅱ)设P是图象上的最高点，M、N是图象与x轴的交点，求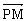与的夹角．

Answer 1

本题主要考查三角函数的图象，已知三角函数值求角，向量夹角的计算等基础知识和基本的运算能力。

  解：（Ⅰ）因为函数图象过点（0，1），

           所以2sinφ=1，即sinφ=.

           因为0≤φ≤，所以φ=.

     （Ⅱ）由函数y=2sin（πx+）及其图象，得

           M（-，0）P（，2）N（），

           所以=（-，），=（，），从而

    =

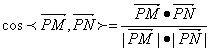
故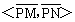=arccos.