题目内容
19.在等腰三角形ABC中,∠A=150°,AB=AC=1,则$\overrightarrow{AB}•\overrightarrow{BC}$=( )| A. | $-\frac{{\sqrt{3}}}{2}-1$ | B. | $-\frac{{\sqrt{3}}}{2}+1$ | C. | $\frac{{\sqrt{3}}}{2}-1$ | D. | $\frac{{\sqrt{3}}}{2}+1$ |
分析 方法一:利用向量的射影即可求出,
方法二:根据向量数量积的公式,余弦定理,两角差的余弦公式即可求出.
解答  解:方法一:如图所示,过点C作CD⊥BA,交于点D,
解:方法一:如图所示,过点C作CD⊥BA,交于点D,
∴$\overrightarrow{AB}•\overrightarrow{BC}$=-$\overrightarrow{BA}$•$\overrightarrow{BC}$=-|$\overrightarrow{BA}$|•|$\overrightarrow{BC}$|cosB=-[|$\overrightarrow{BA}$|+|$\overrightarrow{CA}$|cos(180°-150°)]=-(1+$\frac{\sqrt{3}}{2}$)=-1-$\frac{\sqrt{3}}{2}$
方法二,等腰三角形ABC中,∠A=150°,AB=AC=1,
∴B=15°,
∴cos15°=cos(45°-30°)=$\frac{\sqrt{2}}{2}$×$\frac{\sqrt{3}}{2}$+$\frac{\sqrt{2}}{2}$×$\frac{1}{2}$=$\frac{\sqrt{6}+\sqrt{2}}{4}$
由余弦定理可得BC2=AB2+AC2-2AB•AC•cosA=1+1-2×(-$\frac{\sqrt{3}}{2}$)=2+$\sqrt{3}$,
∴BC=$\sqrt{2+\sqrt{3}}$
∴$\overrightarrow{AB}•\overrightarrow{BC}$=|$\overrightarrow{AB}$||$\overrightarrow{BC}$|cos(180°-15°)=1×$\sqrt{2+\sqrt{3}}$×(-$\frac{\sqrt{6}+\sqrt{2}}{4}$)=-1-$\frac{\sqrt{3}}{2}$
故选:A.
点评 本题主要考查平面向量的基本运算,利用向量的射影和向量数量积,以及余弦定理解决本题的关键.

 一线名师提优试卷系列答案
一线名师提优试卷系列答案| A. | 1 | B. | 0 | C. | -1 | D. | -2 |
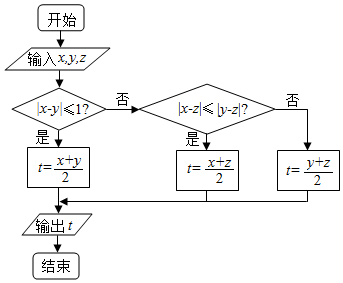
| A. | x=6,y=8,z=9 | B. | x=8,y=7,z=9 | C. | x=8,y=6,z=10 | D. | x=8,y=6,z=8 |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | 2 | B. | 3 | C. | 9 | D. | 11 |
| A. | 30尺 | B. | 90尺 | C. | 150尺 | D. | 180尺 |
| A. | (-∞,-1)∪(-$\frac{1}{9}$,+∞) | B. | (-$\frac{5}{27}$,1) | C. | (-∞,1) | D. | (-∞,-$\frac{5}{27}$)∪(1,+∞) |