题目内容
4.在数列{an}中,“|an+1|>an”是“数列{an}为递增数列”的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
分析 由“|an+1|>an”?an+1>an;或-an+1>an.由数列{an}为递增数列?|an+1|≥an+1>an.即可判断出结论.
解答 解:由“|an+1|>an”?an+1>an;或-an+1>an充分性不成立,
由数列{an}为递增数列?|an+1|≥an+1>an成立,必要性成立,
∴“|an+1|>an”是“数列{an}为递增数列”的必要不充分条件.
故选:B.
点评 本题考查了数列的单调性、不等式的性质、简易逻辑的判定方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
12.椭圆$\frac{x^2}{m}+\frac{y^2}{20}=1$的焦距为8,则m的值等于( )
| A. | 36或4 | B. | 6 | C. | $2\sqrt{21}$ | D. | 84 |
16.将函数f(x)=$\sqrt{3}$cos(πx)图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再把图象上所有的点向右平移1个单位长度,得到函数g(x)的图象,则函数g(x)的单调区间是( )
| A. | [4k+1,4k+3](k∈Z) | B. | [2k+1,2k+3](k∈Z) | C. | [2k+1,2k+2](k∈Z) | D. | [2k-1,2k+2](k∈Z) |
 一几何体的三视图如图所示
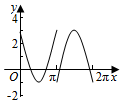
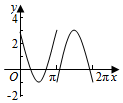
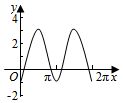
一几何体的三视图如图所示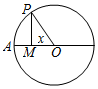 如图,圆O的半径为2,圆上一点P从A出发,绕着点O顺时针方向旋转一周,在旋转的过程中,记∠AOP为x(x∈[0,2π]),P在OA上的射影为M,记f(x)=$\overrightarrow{OP}$•$\overrightarrow{OM}$-1,那么函数f(x)的图象大致为( )
如图,圆O的半径为2,圆上一点P从A出发,绕着点O顺时针方向旋转一周,在旋转的过程中,记∠AOP为x(x∈[0,2π]),P在OA上的射影为M,记f(x)=$\overrightarrow{OP}$•$\overrightarrow{OM}$-1,那么函数f(x)的图象大致为( )