题目内容
19.设实数x,y满足约束条件$\left\{\begin{array}{l}x-2y-3≤0\\ x+2y-3≤0\\ x≥-3\end{array}\right.$,则z=-2x+3y的取值范围是[-6,15].分析 由题意作平面区域,化简z=-2x+3y为y=$\frac{2}{3}$x+$\frac{z}{3}$,从而结合图象求解.
解答  解:由题意作平面区域如下,
解:由题意作平面区域如下,
化简z=-2x+3y为y=$\frac{2}{3}$x+$\frac{z}{3}$,
故结合图象可知,
在点B(3,0)处有最小值,在点C(-3,3)处有最大值,
故-2×3+3×0≤z≤-2×(-3)+3×3,
即z∈[-6,15],
故答案为:[-6,15].
点评 本题考查了线性规划的应用及数形结合的思想应用.

练习册系列答案
相关题目
9.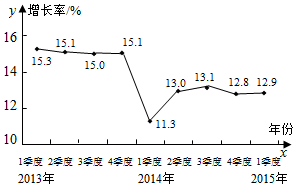 如图是近三年某市生产总值增速(累计,%)的折线统计图,据该市统计局初步核算,2015年一季度全区生产总值为1552.38亿元,与去年同一时期相比增长12.9%(如图,折线图中其它数据类同).根据统计图得出正确判断是( )
如图是近三年某市生产总值增速(累计,%)的折线统计图,据该市统计局初步核算,2015年一季度全区生产总值为1552.38亿元,与去年同一时期相比增长12.9%(如图,折线图中其它数据类同).根据统计图得出正确判断是( )
 如图是近三年某市生产总值增速(累计,%)的折线统计图,据该市统计局初步核算,2015年一季度全区生产总值为1552.38亿元,与去年同一时期相比增长12.9%(如图,折线图中其它数据类同).根据统计图得出正确判断是( )
如图是近三年某市生产总值增速(累计,%)的折线统计图,据该市统计局初步核算,2015年一季度全区生产总值为1552.38亿元,与去年同一时期相比增长12.9%(如图,折线图中其它数据类同).根据统计图得出正确判断是( )| A. | 近三年该市生产总值为负增长 | |
| B. | 近三年该市生产总值为正增长 | |
| C. | 该市生产总值2013年到2014年为负增长,2014年到2015年为正增长 | |
| D. | 以上判断都不正确 |
14.已知椭圆$E:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左右焦点分别是F1,F2,短轴一个端点M(0,b),直线l:4x+3y=0交椭圆E于A,B两点,若|AF1|+|BF1|=6,点M到直线l的距离不小于$\frac{6}{5}$,则椭圆E的离心率范围是( )
| A. | $(0,\frac{{\sqrt{5}}}{3}]$ | B. | $[\frac{{\sqrt{5}}}{3},1)$ | C. | $(0,\frac{{\sqrt{3}}}{2}]$ | D. | $[\frac{{\sqrt{3}}}{2},1)$ |
4.在数列{an}中,“|an+1|>an”是“数列{an}为递增数列”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
8.等比数列{an}中,a1=1,公比q=2,前n项和为Sn,下列结论正确的是( )
| A. | $?{n_0}∈N*,{a_{n_0}}+{a_{{n_0}+2}}=2{a_{{n_0}+1}}$ | |
| B. | ?n∈N*,an•an+1≤an+2 | |
| C. | ?n∈N*,Sn<an+1 | |
| D. | $?{n_0}∈N*,{a_{n_0}}+{a_{{n_0}+3}}={a_{{n_0}+1}}+{a_{{n_0}+2}}$ |
9.所示的程序框图输出的结果为S=35,则判断框中应填入的关于k的条件是( )


| A. | k>7 | B. | k≤6 | C. | k>6 | D. | k<6 |
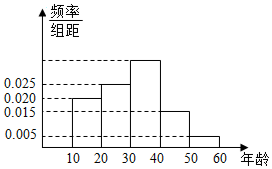 随机抽取100名年龄在[10,20),[20,30)…,[50,60)年龄段的市民进行问卷调查,由此得到样本的频率分布直方图如图所示,从不小于30岁的人中按年龄段分层抽样的方法随机抽取22人,则在[50,60)年龄段抽取的人数为2.
随机抽取100名年龄在[10,20),[20,30)…,[50,60)年龄段的市民进行问卷调查,由此得到样本的频率分布直方图如图所示,从不小于30岁的人中按年龄段分层抽样的方法随机抽取22人,则在[50,60)年龄段抽取的人数为2.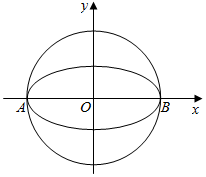 如图,椭圆$W:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率为$\frac{{\sqrt{3}}}{2}$,其左顶点A在圆O:x2+y2=16上.
如图,椭圆$W:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率为$\frac{{\sqrt{3}}}{2}$,其左顶点A在圆O:x2+y2=16上.