题目内容
16.将函数f(x)=$\sqrt{3}$cos(πx)图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再把图象上所有的点向右平移1个单位长度,得到函数g(x)的图象,则函数g(x)的单调区间是( )| A. | [4k+1,4k+3](k∈Z) | B. | [2k+1,2k+3](k∈Z) | C. | [2k+1,2k+2](k∈Z) | D. | [2k-1,2k+2](k∈Z) |
分析 根据图象的变换规则逐步得出函数解析式,利用正弦函数的单调性即可得解.
解答 解:∵将函数f(x)=$\sqrt{3}$cos(πx)图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),得到函数解析式为:y=$\sqrt{3}$cos($\frac{1}{2}$πx);
再把图象上所有的点向右平移1个单位长度,得到函数的解析式为:g(x)=$\sqrt{3}$cos[$\frac{1}{2}$π(x-1)];
∴可得:$g(x)=\sqrt{3}sin\frac{π}{2}x$,
∵由2k$π+\frac{π}{2}$≤$\frac{πx}{2}$≤2kπ+$\frac{3π}{2}$,k∈Z,解得:4k+1≤x≤4k+3,k∈Z,
可得函数g(x)的单调递减区间是:[4k+1,4k+3],k∈Z,
由2kπ-$\frac{π}{2}$≤$\frac{πx}{2}$≤2k$π+\frac{π}{2}$,k∈Z,解得:4k-1≤x≤4k+1,k∈Z,
可得函数g(x)的单调递增区间是:[4k-1,4k+1],k∈Z,
对比各个选项,只有A正确.
故选:A.
点评 本题考查了函数y=Asin(ωx+φ)的图象变换规律,考查了正弦函数的图象和性质,属于基础题.

练习册系列答案
相关题目
4.在数列{an}中,“|an+1|>an”是“数列{an}为递增数列”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
8.等比数列{an}中,a1=1,公比q=2,前n项和为Sn,下列结论正确的是( )
| A. | $?{n_0}∈N*,{a_{n_0}}+{a_{{n_0}+2}}=2{a_{{n_0}+1}}$ | |
| B. | ?n∈N*,an•an+1≤an+2 | |
| C. | ?n∈N*,Sn<an+1 | |
| D. | $?{n_0}∈N*,{a_{n_0}}+{a_{{n_0}+3}}={a_{{n_0}+1}}+{a_{{n_0}+2}}$ |
6.阅读如图所示的程序框图,运行相应的程序.若输出的S为$\frac{25}{24}$,则判断框中填写的内容可以是( )
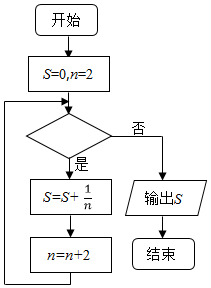

| A. | n=6 | B. | n<6 | C. | n≤6 | D. | n≤8 |
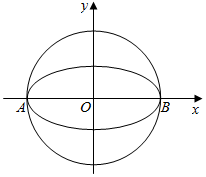 如图,椭圆$W:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率为$\frac{{\sqrt{3}}}{2}$,其左顶点A在圆O:x2+y2=16上.
如图,椭圆$W:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率为$\frac{{\sqrt{3}}}{2}$,其左顶点A在圆O:x2+y2=16上. 某公司从大学招收毕业生,经过综合测试,录用了14名男生和6名女生,这20名毕业生的测试成绩如茎叶图所示(单位:分).公司规定:
某公司从大学招收毕业生,经过综合测试,录用了14名男生和6名女生,这20名毕业生的测试成绩如茎叶图所示(单位:分).公司规定: