题目内容
要测量底部不能到达的电视塔AB的高度,在C点测得塔顶A的仰角是45°,在D点测得塔顶A的仰角是30°,并测得水平面上的∠BCD=120°,CD=40m,求电视塔的高度.
如图,设电视塔AB的高为xm,则在Rt△ABC中,由∠ACB=45°得BC=x.

在Rt△ABD中,∠ADB=30°,
∴BC= x.
x.
在△BDC中,由余弦定理,得
BD2=BC2+CD2-2BC·CD
·cos120°,
即( x)2=x2+402-2·x·40·cos120°,
x)2=x2+402-2·x·40·cos120°,
解得x=40,∴电视塔高为40米.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
铁矿石A和B的含铁率为a,冶炼每万吨铁矿石的CO2的排放量b及每万吨铁矿石的价格c,如下表:
|
| a | b(万吨) | c( 百万元) |
| A | 50% | 1 | 3 |
| B | 70% | 0.5 | 6 |
某冶炼厂至少要生产1.9(万吨)铁,若要求CO2的排放量不超过2(万吨),则购买铁矿石的最少费用为________(百万元).
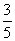 .求sinA的值.
.求sinA的值.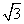 ,∠A=
,∠A= ,则∠C的大小为________.
,则∠C的大小为________. m B.20
m B.20 m
m 米 B.10
米 B.10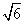 米
米 米 D.20
米 D.20 米
米 则x+2y的最大值是( )
则x+2y的最大值是( ) B.0
B.0 D.
D. ,Q=
,Q= (lga+lgb),R=lg
(lga+lgb),R=lg ,则( )
,则( )