题目内容
4.已知数列{an}的前n项和为Sn,点($\sqrt{{a}_{n}}$,Sn)在曲线y=2x2-2上.(1)求证:数列{an}是等比数列;
(2)设数列{bn}满足bn=$\frac{1}{lo{g}_{4}{a}_{n}•lo{g}_{4}{a}_{n+1}}$,求数列{bn}的前n项和Tn.
分析 (1)通过Sn=2an-2与Sn-1=2an-1-2(n≥2)作差,进而可得数列{an}是首项、公比均为2的等比数列;
(2)通过(1)裂项可知bn=4($\frac{1}{n}$-$\frac{1}{n+1}$),进而并项相加即得结论.
解答 (1)证明:依题意,Sn=2an-2,
∴Sn-1=2an-1-2(n≥2),
两式相减得:an=2an-2an-1,即an=2an-1,
又∵a1=2a1-2,即a1=2,
∴数列{an}是首项、公比均为2的等比数列;
(2)解:由(1)可知an=2n,
∴bn=$\frac{1}{lo{g}_{4}{a}_{n}•lo{g}_{4}{a}_{n+1}}$=$\frac{1}{\frac{n}{2}•\frac{n+1}{2}}$=$\frac{4}{n(n+1)}$=4($\frac{1}{n}$-$\frac{1}{n+1}$),
∴Tn=4(1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+…+$\frac{1}{n}$-$\frac{1}{n+1}$)
=4(1-$\frac{1}{n+1}$)
=$\frac{4n}{n+1}$.
点评 本题考查数列的通项及前n项和,考查裂项相消法,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
14.已知{an}是首项为1的等比数列,若Sn是{an}的前n项和,且28S3=S6,则数列{$\frac{1}{{a}_{n}}$}的前4项和为( )
| A. | $\frac{15}{8}$ | B. | 4 | C. | $\frac{40}{27}$ | D. | 40 |
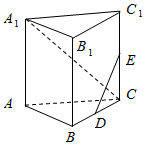 已知三棱柱ABC-A1B1C1,侧棱AA1垂直于底面ABC,∠$ABC=\frac{π}{2}$,AB=BC=AA1=4,D为BC的中点.
已知三棱柱ABC-A1B1C1,侧棱AA1垂直于底面ABC,∠$ABC=\frac{π}{2}$,AB=BC=AA1=4,D为BC的中点.