题目内容
(本小题满分12分)
已知双曲线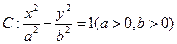 的离心率为
的离心率为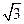 ,右准线方程为
,右准线方程为
(1)求双曲线 的方程;
的方程;
(2)设直线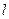 是圆
是圆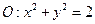 上动点
上动点 处的切线,
处的切线,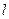 与双曲线
与双曲线 交于不同的两点
交于不同的两点 ,证明
,证明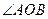 的大小为定值.
的大小为定值.
已知双曲线
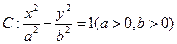 的离心率为
的离心率为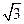 ,右准线方程为
,右准线方程为
(1)求双曲线
 的方程;
的方程;(2)设直线
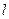 是圆
是圆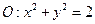 上动点
上动点 处的切线,
处的切线,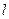 与双曲线
与双曲线 交于不同的两点
交于不同的两点 ,证明
,证明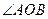 的大小为定值.
的大小为定值.(1)
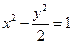
(2)证明略
(1)由题意,得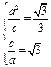 ,解得
,解得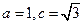 ,
,
∴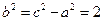 ,∴所求双曲线
,∴所求双曲线 的方程为
的方程为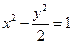 . ……… (5分)
. ……… (5分)
(2)点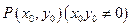 在圆
在圆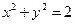 上,
上,
圆在 点
点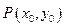 处的切线方程为
处的切线方程为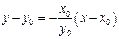 ,
,
化简得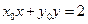 .由
.由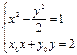 及
及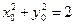 得
得
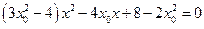 ①
①
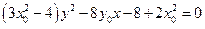 ②
②
∵切线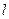 与双曲线C交于不同的两点A、B,且
与双曲线C交于不同的两点A、B,且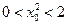 ,
,
∴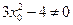 ,设A、B两点的坐标分别为
,设A、B两点的坐标分别为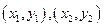 ,
,
则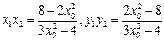 ,∴
,∴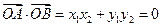 ,∴
,∴ 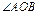 大小为
大小为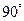 .(12分)
.(12分)
(∵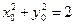 且
且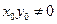 ,∴
,∴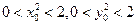 ,
,
从而当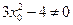 时,方程①和方程②的判别式均大于零).
时,方程①和方程②的判别式均大于零).
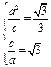 ,解得
,解得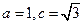 ,
,
∴
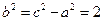 ,∴所求双曲线
,∴所求双曲线 的方程为
的方程为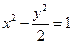 . ……… (5分)
. ……… (5分)(2)点
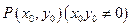 在圆
在圆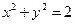 上,
上,圆在
 点
点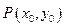 处的切线方程为
处的切线方程为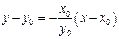 ,
,化简得
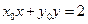 .由
.由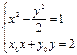 及
及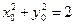 得
得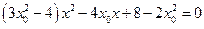 ①
①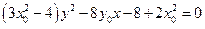 ②
②∵切线
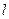 与双曲线C交于不同的两点A、B,且
与双曲线C交于不同的两点A、B,且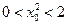 ,
,∴
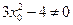 ,设A、B两点的坐标分别为
,设A、B两点的坐标分别为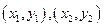 ,
,则
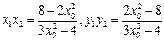 ,∴
,∴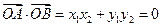 ,∴
,∴ 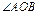 大小为
大小为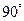 .(12分)
.(12分)(∵
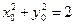 且
且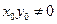 ,∴
,∴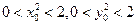 ,
,从而当
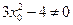 时,方程①和方程②的判别式均大于零).
时,方程①和方程②的判别式均大于零).
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 与直线
与直线 +3有两个不同的公共点,则实数 k 的取值范围是( )
+3有两个不同的公共点,则实数 k 的取值范围是( )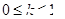
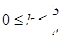
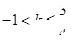
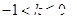
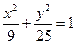 共焦点,他们的离心率之和为
共焦点,他们的离心率之和为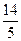 ,求双曲线的标准方程
,求双曲线的标准方程 的右焦点是抛物线的焦点,则抛物线的标准方程是 ▲ .
的右焦点是抛物线的焦点,则抛物线的标准方程是 ▲ . 的右支上,若点A到右焦点的距离为2x0,则
的右支上,若点A到右焦点的距离为2x0,则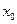 =" "
=" " 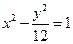 上的一点,
上的一点,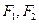 是该双曲线的两个焦点,若
是该双曲线的两个焦点,若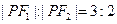 ,则
,则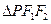 的面积为___________.
的面积为___________. 的离心率为
的离心率为 ,左、右两焦点分别为
,左、右两焦点分别为 ,抛物线
,抛物线 以
以 为顶点,
为顶点, 为焦点,点
为焦点,点 为抛物线与双曲线右支的一个交点,若
为抛物线与双曲线右支的一个交点,若 ,则
,则



 表示的图形是双曲线,则
表示的图形是双曲线,则 的取值范围 为 .
的取值范围 为 .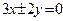 ,则该双曲线的离心率等于_____
,则该双曲线的离心率等于_____