题目内容
19.已知cosα=$\frac{1}{4}$,且α∈($\frac{3π}{2}$,2π),则cos( α+$\frac{π}{2}$)=$\frac{\sqrt{15}}{4}$.分析 由条件利用同角三角函数的基本关系、诱导公式求得cos( α+$\frac{π}{2}$)的值.
解答 解:∵cosα=$\frac{1}{4}$,且α∈($\frac{3π}{2}$,2π),则cos( α+$\frac{π}{2}$)=-sinα=$\sqrt{{1-cos}^{2}α}$=$\sqrt{1-\frac{1}{16}}$=$\frac{\sqrt{15}}{4}$,
故答案为:$\frac{\sqrt{15}}{4}$.
点评 本题主要考查同角三角函数的基本关系、诱导公式的应用,属于基础题.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
10.设实数x,y满足约束条件$\left\{\begin{array}{l}x≥0\\ x≥y\\ 2x-y≤1\end{array}\right.$,则${8^x}•{(\frac{1}{4})^{-y}}$的最大值是( )
| A. | 64 | B. | 32 | C. | 2$\sqrt{2}$ | D. | 1 |
7.已知复数$z=\frac{{{{(1-i)}^2}}}{1+i}$(i为虚数单位),则复数z=( )
| A. | 1+i | B. | 1-i | C. | -1+i | D. | -1-i |
14.已知1<a<2,则函数f(x)=ax-2的零点属于区间( )
| A. | (1,2) | B. | (2,4) | C. | $(\frac{1}{2},1)$ | D. | $(\frac{1}{4},\frac{1}{2})$ |
11.已知函数$f(x)=\left\{\begin{array}{l}{log_2}(2-x),0≤x<k\\{x^3}-3{x^2}+3,k≤x≤a\end{array}\right.$.若存在实数k使得函数f(x)的值域为[-1,1],则实数a的取值范围是( )
| A. | $[\frac{3}{2},1+\sqrt{3}]$ | B. | $[2,1+\sqrt{3}]$ | C. | [1,3] | D. | [2,3] |
8.为了解某市市民的节能意识及行为习惯等情况,某机构在市区范围内进行了一次有关市民节能意识及行为习惯的测试,将所有参加者的笔试成绩(得分均为整数,满分为100分)进行统计,绘制成如下的频数分布表:
(1)若采用分层抽样的方法从分数在[60,70)内和[90,100]内的参加者中抽取5人做问卷调查,求这5人中分数在[90,100]内的人数;
(2)在(1)的条件,从抽取的5人中再随机选取3人进行跟踪调查,记分数在[60,70)内的人数为X,求随机变量X的分布列和数学期望.
| 分数(分数段) | 频数(人数) |
| [60,70) | 9 |
| [70,80) | 19 |
| [80,90) | 16 |
| [90,100] | 6 |
| 合计 | 50 |
(2)在(1)的条件,从抽取的5人中再随机选取3人进行跟踪调查,记分数在[60,70)内的人数为X,求随机变量X的分布列和数学期望.
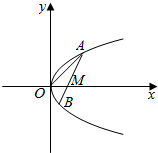 如图,线段AB过x轴正半轴上一定点M(m,0),端点A、B到x轴距离之积为2m,以x轴为对称轴,过A,O,B三点作抛物线C.
如图,线段AB过x轴正半轴上一定点M(m,0),端点A、B到x轴距离之积为2m,以x轴为对称轴,过A,O,B三点作抛物线C.