题目内容
17．已知数列{an}、{bn}满足bn=log2an，n∈N+，其中{bn}是等差数列，且a9a2009=4，则b1+b2+b3+…+b2017=（ ）| A． | 2016 | B． | 2017 | C． | log22017 | D． | $\frac{2017}{2}$ |
分析 由已知得an=2${\;}^{{b}_{n}}$，计算$\frac{{a}_{n+1}}{{a}_{n}}$可判断{an}为等比数列，于是a1a2017=a9a2009=4，从而得出b1+b2017=2，代入等差数列的求和公式即可．
解答 解：设{bn}的公差为d，
∵bn=log2an，∴an=2${\;}^{{b}_{n}}$，
∴$\frac{{a}_{n+1}}{{a}_{n}}$=$\frac{{2}^{{b}_{n+1}}}{{2}^{{b}_{n}}}$=2${\;}^{{b}_{n+1}-{b}_{n}}$=2d．
∴{an}是等比数列，
∴a1a2017=a9a2009=4，
即2${\;}^{{b}_{1}}$•2${\;}^{{b}_{2017}}$=2${\;}^{{b}_{1}+{b}_{2017}}$=4，
∴b1+b2017=2，
∴b1+b2+b3+…+b2017=$\frac{{b}_{1}+{b}_{2017}}{2}×2017$=2017．
故选B．
点评 本题考查了等差数列，等比数列的性质，前n项和公式，属于中档题．
练习册系列答案
阳光考场单元测试卷系列答案
名校联盟冲刺卷系列答案
名校提分一卷通系列答案
相关题目
8．一本新出版的数学活动课教材在某书店销售，按事先拟定的价格进行5天试销，每种进价试销1天，得到如下数据：
（Ⅰ）若y与x线性相关，且回归直线方程为y=mx+132，求实数m的值；
（Ⅱ）预计以后的销售中，销量与单价服从（Ⅰ）中的回归直线方程，若每本数学活动课教材的成本是14元，为了获得最大利润，该教材的单价应为多少元？
| 单价x（元） | 18 | 19 | 20 | 21 | 22 |
| 销量y（册） | 61 | 56 | 50 | 48 | 45 |
（Ⅱ）预计以后的销售中，销量与单价服从（Ⅰ）中的回归直线方程，若每本数学活动课教材的成本是14元，为了获得最大利润，该教材的单价应为多少元？
5．已知点P是△ABC的中位线EF上任意一点，且EF∥BC，实数x，y满足$\overrightarrow{PA}+x\overrightarrow{PB}+y\overrightarrow{PC}=\overrightarrow 0$，设△ABC，△PBC，△PCA，△PAB的面积分别为S，S1，S2，S3，记$\frac{S_1}{S}={λ_1}$，$\frac{S_2}{S}={λ_2}$，$\frac{S_3}{S}={λ_3}$，则λ2•λ3取最大值时，3x+y的值为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{3}{2}$ | C． | 1 | D． | 2 |
12．空间直角坐标系中，下列点在x 轴上的是（ ）
| A． | （0.1，0.2，0.3） | B． | （0，0，0.001） | C． | （5，0，0） | D． | （0，0.01，0） |
2．四个数40.2，30.5，30.4，log0.40.5的大小顺序是（ ）
| A． | ${4^{0.2}}＜{3^{0.4}}＜{log_{0.4}}0.5＜{3^{0.5}}$ | B． | ${log_{0.4}}0.5＜{3^{0.4}}＜{4^{0.2}}＜{3^{0.5}}$ | ||
| C． | ${log_{0.4}}0.5＜{3^{0.5}}＜{4^{0.2}}＜{3^{0.4}}$ | D． | ${log_{0.4}}0.5＜{4^{0.2}}＜{3^{0.4}}＜{3^{0.5}}$ |
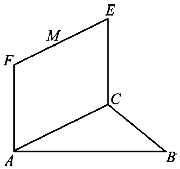如图，矩形ACEF和等边三角形ABC中，AC=2，CE=1，平面ABC⊥平面ACEF．
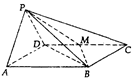如图，在四棱锥中P-ABCD中，底面ABCD是菱形，且∠DAB=60°，PA=PD，M为CD的中点，平面PAD⊥平面ABCD．